AbstractPiezoelectric materials are essential parts of the electronics and electrical equipment used for consumer and industrial applications, such as ultrasonic piezoelectric transducers, sensors, actuators, transformers, and resonators. In this review, the development of piezoelectric materials and the figures of merit for various electromechanical applications are surveyed, focusing on piezoelectric crystals, i.e., the high-performance relaxor-PbTiO3-based perovskite ferroelectric crystals and nonferroelectric high-temperature piezoelectric crystals. The uniqueness of these crystals is discussed with respect to different usages. Finally, the existing challenges and perspective for the piezoelectric crystals are discussed, with an emphasis on the temperature-dependent properties, from cryogenic temperatures up to the ultrahigh-temperature usage range.
1. IntroductionThe piezoelectric effect is a phenomenon by which certain dielectric materials (with non-center symmetries, excluding the 432 point group) generate an electric charge in response to applied mechanical stress (direct piezoelectric effect), or generate mechanical strain/displacement under an applied electric field (converse piezoelectric effect).1) Piezoelectric materials lie at the heart of electromechanical devices. Applications include actuators, ultrasonic imaging, high-intensity focused ultrasound, underwater acoustic ultrasound, nondestructive evaluation transducer for structural health monitoring (SHM), pressure sensors, and accelerometers to name a few, as shown in Fig. 1. Some of the devices use the converse piezoelectric effect, such as actuators or injectors, and some use the direct piezoelectric effect, such as sensors or hydrophones, whereas most of the electromechanical devices take the advantage of both the direct and converse piezoelectric effects. For example, the ultrasound transducers and surface acoustic wave (SAW)/bulk acoustic wave (BAW) sensors are in the latter group. The generally used piezoelectric materials include bulk ceramics, 2,3) single crystals,4-7) thin films,8-10) textured ceramics,11-13) polymers14,15) and composites.16-18) Of these, the relaxor-PbTiO3-based ferroelectric single crystals with perovskite structure, such as Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT) and Pb(Zn1/3Nb2/3)O3-PbTiO3 (PZN-PT), have attracted extensive attention over the last 20 years, owing to their high piezoelectric properties. The longitudinal piezoelectric strain coefficient d33 and electromechanical coupling factor k33, being on the order of > 1500 pC/N and ~ 90%, respectively, far out-perform the state-of-art polycrystalline ceramics Pb(Zr,Ti)O3 (PZT), thereby showing great promise for various electromechanical applications.5,6,19,20)
There are many different medical imaging modalities, such as radiography, magnetic resonance imaging (MRI), computed tomography (CT), elastography, photoacoustic imaging, and ultrasound, etc. Of these, medical ultrasound uses high-frequency broadband transducers, with the advantages of real-time monitoring of moving structures and no ionizing radiation, etc. Ultrasonic transducers convert electrical energy into a mechanical form when generating an acoustic wave (transmitter) and convert mechanical energy into an electrical signal when detecting the echo (receiver). As underwater acoustic technology matured, it began to have significant commercial applications such as depth sounding to provide detailed ocean bottom mapping. 21) Bottom mapping techniques can be readily extended to the exploration of the underwater oil/gas or mineral mining, underwater cable or pipeline inspections, and oceanographic research. In addition, it also has commercial importance in the fishing industry, where transducers were developed specifically for locating schools of fish. The relaxor-PT single crystals have been successfully commercialized in medical imaging, while being extensively studied for underwater acoustic applications.20)
Most electromechanical devices operate over a temperature range of −50~150°C, whereas high-temperature sensing is of great and increasing interest for applications in aerospace, automotive, power plants, and material processing. Table 1 lists the key features of existing high-temperature sensors.22) Fiber optic sensors have been used to measure strain, displacement, temperature, and other physical quantities, because of the ease of embedment, immunity to electromagnetic interference (EMI), and potential for assembling multiple sensors in a single fiber, but this type of sensor is still in the developmental stage for damage detection in the ultrasonic frequency range. Piezoresistive sensors utilize the electrical resistance change in response to external excitations such as force, pressure, or acceleration. In general, piezoresistive sensors are less susceptible to EMI. However, the inherent temperature dependence of material resistivity can lead to inaccuracies for ultrahigh-temperature applications. Capacitive sensors have the advantages of low thermal drift, high resolution, and good noise performance. However, this type of sensor suffers from limited robustness and is easily impacted by parasitic capacitance with magnitudes similar to that of the sensor itself. Electrical strain gauges are widely used because they are inexpensive, easy to install and sensitive to detect low-frequency strain signals, but are susceptible to ambient noise frequencies, inaccessible to remote areas, and exhibit a fragile nature. Of particular interest are the piezoelectric sensors, which have been widely used for SHM applications. This is owing to their wide bandwidth, versatility, simplicity, high rigidity, high stability, high reproducibility, fast response time, wide operating temperature range, insensitivity to electric and magnetic fields, capacity for miniaturization, minimal dependence on moving parts, low power consumption, as well as the wide piezoelectric material and mechanism selections, which greatly benefit the SHM device design.22)
2. History of Piezoelectric Materials
Figure 2 gives a brief history and milestones of the development of piezoelectric materials, including the ferroelectric materials and nonferroelectric piezoelectric crystals.20,23,24)
The piezoelectric effect was first discovered in 1880 by Pierre and Jacques Curie in piezoelectric quartz crystals. Quartz possesses excellent electrical resistivity, ultrahigh mechanical Q, and high temperature-stability, making it a material of choice in telecommunication equipment. The piezoelectric coefficient is low, being d11 ~ 2.3pC/N, with a low α-β phase transition temperature at 573°C, which is further restricted by its mechanical twinning at 300°C.25) Rochelle salt crystal was first synthesized in 1655, but its ferroelectricity and subsequent piezoelectric nature were demonstrated later by Valasek in 1921, showing a strong piezoelectric effect.25,26) However, Rochelle salt was found to be hygroscopic and show strong temperature-dependent behavior (Curie point of 23°C). The motivation for exploring new man-made piezoelectric materials led to the discovery and development of potassium dihydrogen phosphate (KDP) and ammonium dihydrogen phosphate (ADP) crystals in 1935 and the early 1940s, showing relatively strong piezoelectric activity, with 23 and 49 pC/N, respectively. The ADP crystals were then established for high-power acoustic transducers, replacing Rochelle salt.20)
In the early 1940s, a breakthrough was achieved by the use of ferroelectrics with a perovskite structure. The first of these ferroelectrics, barium titanate (BaTiO3) (BT), was discovered independently by Von Hippel and Goldman. The first BT crystal was grown in 1947 and the piezoelectric coefficient d33 was reported to be 86 pC/N, which was much lower than its polycrystalline counterpart, at 190 pC/N.27) The milestone studies, which established the perovskite PZT system as exceptionally suitable piezoelectric material formulations, were carried out by Jaffe et al., who discovered that the nearly temperature-independent morphotropic phase boundary (MPB) in PZT was vitally important for piezoelectric applications, owing to the high piezoelectric properties near the MPB compositions.28) The leading position of PZT compositions was owing to their strong piezoelectric effect and relatively high Curie temperature. PZTs also allow a wide variation in chemical modification to tailor a broad range of operating parameters without a serious reduction in the piezoelectric effect, where the chemical dopants included isovalent substitutes of the lead cation by base earth elements, acceptor or donor dopants on the A or B sites of the perovskite structrue.3,29) A series of formulations labeled PZT (PZT4, PZT5A, PZT5H, PZT8, etc.) have been established to emphasize various properties. Fig. 3 compares the “hard” and “soft” PZT ceramics, which have been extensively used for more than 60 years.29-31) Undoubtedly, the PZT family is, by far, the most important and versatile compositional base for piezoelectric elements.
A search for ferroelectric materials that can be used at elevated temperatures has stimulated interest in the family of bismuth layer-structured ferroelectrics (BLSF), which was first discovered by Aurivillius in 1949. The general formula of BLSF is (Bi2O2)2+(Am−1BmO3m+1)2−, which can be described as regular stacking of (Am−1BmO3m+1)2− pseudo-perovskite blocks, separated by fluorite-like (Bi2O2)2+ layers along the c-axis. 32,33) The (Bi2O2)2+ act as insulating paraelectric layers, limiting the spontaneous polarization of BLSF materials in the a-b plane, i.e., the pseudo-perovskite (Am−1BmO3m+1)2− blocks. The BLSFs present low dielectric permittivities, low aging rates, strong anisotropic electromechanical properties, high mechanical quality factors, and high Curie temperatures, and thus are promising candidates for high-temperature sensor applications. Piezoelectric activity in BLSFs can be further improved by suitable doping, while enhancing the electrical resistivity and achieving a compromise between good polarizability and a high Curie temperature. 34-41) Piezoelectric single crystals of LiNbO3 (LN) and LiTaO3 (LT) were synthesized for the first time in Bell laboratories in 1967.42) Both crystals have an ilmenite structure and are well known for their low acoustic losses, and thus they are excellent materials for SAW devices. LN possesses a number of useful orientation-controlled crystal cuts, which are now extensively used in piezoelectric applications, including compression 36°-rotated y-cut and shear 163°-rotated y-cut.20)
Different from ferroelectric ceramics/crystals, polyvinylidene fluoride (PVDF) polymers, which were first reported in 1969, are strong candidates for new sensors that cannot be realized with piezoceramics or single crystals.43,44) The unique inherent properties, such as high sensibility (piezoelectric d coefficient of 20-30 pC/N, high piezoelectric g coefficient typically one order higher than that of piezoceramics), high compliance (high flexibility), high mechanical resistance, light weight (low density), low acoustic impedance, broadband acoustic performance, and availability in large area, have made them suitable for many sensing applications involving complicated shapes and significant structural strains.45) In the 1970s, it was deemed that further improvements in the performance of established piezoelectrics were not forthcoming. Thus, various piezoelectric composites were introduced by Newnham in 1978, through the concept of “engineered biphasic connectivity.”16) The particular significance of piezoelectric composites is that the structurally and compositionally homogeneous ceramics and single crystals can be combined with a passive polymer material to form composites, increasing the material flexibility and improving the acoustic impedance matching between the active material and the medium in which the acoustic wave travels. By structurally combining a piezoelectric ceramic and a polymer with certain connectivity, the resulting composite material can successfully integrate the advantages of both materials. Several interesting connectivity patterns were developed, including 0-3, 1-3, and 2-2 structures, and are now being widely employed in transducer applications.46,47)
Another important piezoelectric material category is that of relaxor-based perovskite ferroelectrics, which exhibit local structural heterogeneity, i.e., a polar nanoregion (PNR), leading to extremely large dielectric permittivity.25,48-55) One such material is lead magnesium niobate (PMN). Of particular importance is the report of a single-crystal PMN-PT solid solution in the early 1990s. Systematic studies on the piezoelectric properties of PMN-PT crystals poled along different crystallographic directions were reported in the late 1990s and early 2000s, showing ultrahigh piezoelectric coefficients and electromechanical coupling factors, on the order of > 1500 pC/N and > 90%, which far outperformed the state-of-art ferroelectric PZT ceramics, and triggered interest in the crystals and their applications.56,57) The existence of local structural heterogeneity was thought to be responsible for the high dielectric and piezoelectric properties in relaxor-PT crystals.58-69) Extensive efforts have focused on relaxor-PT crystal systems, including binary systems PMN-PT, PZN-PT, Pb(Sc0.5Nb0.5)O3-PbTiO3,70) Pb(Yb0.5Nb0.5)O3-PbTiO3,71,72) Pb(In0.5Nb0.5)O3-PbTiO3,73,74) and BiScO3-PbTiO3,75,76) and ternary systems Pb(In0.5Nb0.5)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 (PIN-PMN-PT),77-92) Pb(Mg1/3Nb2/3)O3-PbZrO3-PbTiO3,93-98) etc.
Generally speaking, perovskite ferroelectric materials possess high piezoelectric properties owing to the fact that the perovskite ferroelectrics exhibit different ferroelectric phases with minimal energy discrepancies, leading to a high dielectric constant in a strong polar lattice in the proximity of the phase boundary, including an MPB, polymorphic phase boundary, or tricritical point.99-105) However, nonferroelectric piezoelectric crystals exhibit low piezoelectric properties, being in the range of single digits or low tens of pC/N.7,23,106-113) For example, quartz is the best known and the first piezoelectric crystal, with piezoelectric coefficient of 2.3 pC/N. Various nonferroelectric piezoelectric crystals have been extensively researched for high-temperature applications, including quartz (SiO2), gallium orthophosphate (GaPO4),114-119) melilite,111,120,121) sillenite,122) fresnoite, 123-125) langasite (La3Ga5SiO14, LGS),109,110,126-136) and oxyborate crystals.137-144) Each of these materials has its own unique advantages and drawbacks for use in high-temperature sensors.
3. Crystal Fabrication MethodsThe growth of bulk single crystals from liquid/solid state plays a dominant role for many technical applications and also in basic research. Numerous crystal growth techniques have been developed to obtain single crystals.145) These techniques include growth from high-temperature solutions (flux; top seeded solution growth (TSSG); Kyropoulos), from the pure melt (Bridgman; Stockbarger; Czochralski (Cz); floating-zone melting, etc.); from vapor (such as chemical vapor deposition; physical vapor transport; sublimation); from aqueous or nonaqueous solvent; hydrothermal and solid-state crystal growth (SSCG), etc.
Figure 4 gives the basic types of binary phase diagrams responsible for the abovementioned growth processes.145) For materials with congruent melting composition/point, the composition of the melt is identical to the solid crystalline phase, and thus they can be grown using Bridgman and/or Cz methods. For the solid-solution system, the crystals can be grown directly from the melt, but compositional segregation occurs during the growth and needs to be taken care of. A distinctive feature in the crystal growth of materials with incongruent melting composition, however, is the composition difference between the liquid and solid phases, especially at the liquid/solid interface; in such cases, special attention is needed, such as controlling the thermal gradient at the growing interface, slowly lowering the temperature in order to force the crystallization, etc. This type of material can be grown using Cz and Bridgman methods, and other growth methods, such as high-temperature solution, including the TSSG and travelling heater method, can also be employed. The crystal growth of eutectic compounds can be high-temperature solution methods, but special attention must be focused on the reduction of inclusions, which is induced by the incorporation of solvent or a flux component. In the following, we briefly survey the most accepted crystal growth methods, and discuss their advantages and disadvantages.
The Cz pulling method was first developed as a technique for growing single crystals of germanium at Bell Laboratories in 1949. This technique originates from pioneering work by Czochralski in 1917.146) In this technique, crystals are grown directly from the melt, initiated from an oriented crystal seed with the same crystal structure and the same/ higher melting temperature than the grown crystal, which is attached to the melt to form a meniscus at the three phase boundary. The crystal can be obtained by slowly pulling up the seed from the melt at a specific rotation speed, with the dimension of the crystal controlled by adjusting the temperature of the melt and the pulling rate. The thermal gradient at the growth interface is generally controlled to be approximately 20-50°C/cm. Other methods, such as TSSG and Kyropoulos, are similar to Cz methods, apart from the solution. The pulling rate of these two techniques is much lower and the thermal gradient at the growth interface is small, compared to the Cz method.147-150) Analogous to Cz crystal growth, the Bridgman method also grows single crystals directly from the melt, which is the most straightforward and economical way to grow high-quality and large-size crystals. The pioneering work by Bridgman was directed toward the growth of single crystals, where he used a vertically mounted tubular electric furnace to melt the charge and lowered the ampoule containing the charge through an axial thermal gradient, such that the molten ingot is gradually crystallized from one end to the other.146) The thermal gradient at the growth interface in the Bridgman method is usually in the range 20-30°C/cm.
In the crystal growth from the high-temperature solution method,146) the constituents of the material to be crystallized are dissolved in a suitable solvent and crystallization occurs as the solution becomes critically supersaturated. The advantage of using a solvent is that crystal growth occurs at a lower temperature than that required for growth from the melt. Thus, this method is candidate for growing the crystals from materials that are incongruently melting, undergo a phase transition below the melting point, which results in severe strain or cracking, possess very high vapor pressure at the melting point, or highly refractory materials. In addition, PZN-PT can only be grown from the high-temperature solvent (flux and/or solution Bridgman methods),151-158) owing to the fact that PZN-PT with a perovskite phase is not stable at high temperature, where the PZN-PT will decompose to a pyrochlore phase. In order to eliminate or reduce spontaneous nucleation points, a local cooling arrangement, such as thin metal rod or metal wire, and controlled oxygen gas flow, are used at the bottom center of the Pt crucible. The thermal gradient is usually approximately 10°C/ cm at the cooling spot. The disadvantages of this method, however, are substitutional or interstitial incorporation of solvent ions into the crystal, microscopic or macroscopic inclusions of solvent or impurities, nonuniform doping, etc.
The SSCG method has been studied as an alternative approach to achieve single crystals.159-168) In the SSCG process, a small single crystal seed is diffusion-bonded to a highly dense polycrystalline body. Growth occurs by consuming fine matrix grains to become a large single crystal after a long annealing period, at temperatures 100-200°C below their respective melting points. This method can be applied to single crystals with highly volatile components, crystals possessing incongruent melting feature, and destructive phase transformation, etc. Because the SSCG method does not involve melting and re-solidification of the ceramic powder, problems such as compositional variations in crystals can be avoided.159) Other methods, such as hydrothermal growth, can also be used for piezoelectric crystal growth, including quartz crystal and its analogues.
4. Figure of Merit of Piezoelectric Materials for Electromechanical Applications
Figure 5 gives a schematic figure showing the material properties related to electromechanical device performance.
From a material viewpoint, different figures of merit (FOMs) have been considered for various applications.19) For example, actuator applications require large piezoelectric strain coefficients with large nonhysteretic strain levels, to achieve large displacements under an external drive field, whereas transducer applications need an FOM of electromechanical coupling factor and dielectric permittivity, in order to achieve broad bandwidth and high sensitivity.20) The broad bandwidth response corresponds to a short pulse length, resulting in a better axial resolution that is dominated by the high electromechanical coupling factor, acoustic impedance, and electrical impedance matching.169) In addition, the electrical impedance of the transducer needs to be matched to the resistance of the coaxial cable and electrical circuit, which is generally 50 Ω. The electrical impedance is inversely associated with the capacitance of the transducer, and thus determined by the clamped dielectric permittivity of the piezoelectric element.170) Low dielectric loss is important for devices operating at off-resonance frequency, accounting for the low heat generation,171-173) whereas mechanical loss is critical for devices operating at resonance frequency, because the acoustic power output is closely associated with the mechanical quality factor.174-184) In addition, a high coercive field is necessary for applications under high-drive conditions, which will improve the field stability and simplify the device design (for example, dc bias may be required to stabilize the poling status of PMN-PT crystals for transducer applications, owing to their low coercive fields).185-189) In addition to the FOMs of materials for high-power transducer applications, other factors also need to be considered for underwater acoustic transducers. For example, it is desired that the underwater transducers operate in the low-frequency range with miniaturized dimensions, high drive fields, and high duty cycles. Furthermore, as with other electroacoustic transducers, a prestress is required for the underwater transducer package, thus affecting the piezoelectric behavior. For all applications, ferroelectric materials with high Curie temperatures are desired, because the ferroelectric crystals with higher Curie temperatures are found to possess expanded operating temperature ranges with less temperature-dependent properties. Thus, the high Curie temperature, together with the MPB and polymorphic phase transitions of the ferroelectric materials will impact the final device reliability and stability.
The piezoelectric sensing technologies for use at ultrahigh temperatures (> 600°C) are in great demand, particularly in the automotive, aerospace, and energy industries.22,190,191) To ensure structural integrity and hence maintain safety and low costs, SHM is expected to play a critical role for detecting, locating, and identifying the sudden and progressive damage and preventing catastrophic structural failure of aerospace components operating in harsh working environments. 192,193) The damages occurred in aerospace structures include, but are not limited to fatigue damage/cracking, corrosion, debonding, delamination, impact damage, and manufacture-induced damage, etc. These damages will significantly change the stiffness, mass, and energy dissipation properties of the structure, which in turn change its dynamic response. This will require different monitoring techniques. As an example, in an aerospace propulsion system, high-temperature (HT) sensors are necessary for intelligent propulsion system design and operation, and for the enhancement of system maintenance, enabling safer, more fuel efficient, and more reliable vehicles for aeronautics and space transportation.194,195) Among various sensing applications, combustion sensors or knock sensors are subject to the harshest environments, because these sensors need to be located as close as possible to the high-temperature source (e.g., combustion engine) for accurate monitoring.196) These sensors are usually required to work properly at temperatures greater than 1000°C, and with vibration sweeping up to 10 g for a relatively long time.192) Moreover, the energy and manufacturing industries consistently demand high-temperature sensing techniques. For example, the nuclear power industry adopts ultrasonic transducers at high temperatures for various nondestructive testing (NDT) and nondestructive evaluation (NDE) of critical components, in order to obtain the internal state of materials or structures.197) In manufacturing plants, ultrasonic NDT of metal components is usually performed at temperatures > 400°C. Therefore, HT sensors are in critical need in a broad range of industries, as well as in new materials development and scientific studies. In addition to the temperature usage range, piezoelectric sensors must survive the harsh environments encountered in space, engines, and power plants, and meanwhile need to possess high sensitivity, resistivity, reliability, stability, and robustness,7,198) as shown in Fig. 6.
5. State-of-the-art of Piezoelectric Crystals5.1. High-performance relaxor-PT ferroelectric crystalsWith the development of relaxor-PT single crystals, in 2010, the concept of various generation crystals was proposed by Smith.5) First-generation crystals exhibit high electromechanical coupling and piezoelectric coefficients that produce transducers with larger bandwidth (× 2-3), higher sensitivity (+12 dB) and higher source level (+12 dB) when compared with the state-of-art polycrystalline ceramic technology, which have already been commercialized in medical ultrasonic transducers. Second-generation crystals extend the high electromechanical properties to a broader range of temperature, electric field, and mechanical stress, expanding their design envelope by reducing the need for heat shunts and applied electric fields. Crystals with higher ferroelectric phase transition temperatures and higher coercive fields are in this category. Third-generation crystals include the addition of small amounts of dopants, to tailor the crystal’s electromechanical parameters and meet the specific device requirements.5) Table 2 compiles the properties of the three generations of crystal systems,5,6,79,82,177,178,199,200) where the TC/TRT and EC of 2nd generation crystals are found to be higher when compared to their 1st generation crystal counterparts, with comparable piezoelectric properties. In addition, the mechanical quality factor of 3rd generation crystals is found to be > 5 times higher than that of 1st generation crystals, owing to the existence of an internal bias. Table 3 to Table 6 compare the relaxor-PT single crystals with those of PZT-based polycrystalline ceramics, with respect to different electromechanical applications, considering their main FOMs.
In addition to their good properties, crystals exhibit several unique properties that are not achievable in polycrystalline ceramics, which thus greatly broaden their usage scope. In the following, the uniqueness of relaxor-PT crystals, including crystallographic anisotropy, high electromechanical coupling, and cryogenic properties are briefly surveyed.
Figure 7 shows the principle piezoelectric properties of poled ceramics compared to rhombohedral PMN-PT single crystals poled along different crystallographic directions, showing the uniqueness of the strong anisotropic characteristics. Poled polycrystalline ceramics are in symmetry, with the piezoelectric matrix the same as 6 mm symmetry. In contrast to ceramics, relaxor-PT single crystals are in macroscopic 4mm, mm2, and 3m symmetries when poled along their crystallographic [001], [011], and [111] directions respectively, leading to strong anisotropic characteristics in their functionalities.201-204)
For PMN-PT crystals with 4R-engineered domain configuration, i.e., poled along the [001] crystallographic direction, an ultrahigh longitudinal piezoelectric coefficient > 1500 pC/N is achieved with a high electromechanical coupling factor of > 90%, taking advantage of the ultrahigh thickness shear piezoelectric coefficient > 2000 pC/N in the 1R single domain state. Of particular significance is that the 2R domain configuration, which exists in the [011] poled rhombohedral crystals, exhibits high longitudinal, thickness shear, and transverse piezoelectric activities simultaneously. In the 2R domain configuration, there are two independent thickness shear piezoelectric coefficients, d15 and d24, and two transverse piezoelectric coefficients, d31 and d32, where d15 >> d24 and −d32 >> d31, because the contribution of the polarization rotation to the shear deformation S4 and extensional deformation S1 in 71° domains negate one another. The very large extensional d32 value, being on the order of −1800 pC/N, gives rise to large in-plane displacement, which is of great interest for actuation applications such as flexural transducers.205-207) This in-plane displacement has also been actively studied, generating interesting physical phenomena owing to the strain-induced magneto-striction and superconductivity,208,209) to name a few. Furthermore, a new face shear (contour shear) vibration mode with high piezoelectric coefficient d36 can also be achieved in rotated 2R crystals (ZXt45° cut),199,210-212) leading to a unique feature of relaxor-PT crystals not achievable in ceramics. In contrast to conventional thickness shear d15, the face shear vibration mode can be repolarized; i.e., the poling electrode is the same as the active electrode. The ac driving field level of the face shear mode was reported to be significantly higher compared to thickness shear vibration modes, owing to the working electrodes along the same direction as that of the polarization. Furthermore, the controlling dimension of the face shear is the length of the sample, rather than the thickness dimension as observed in thickness shear, which thus gives rise to a lower operation frequency on the same dimension. Together with the high d36, k36 and s66 E make it potential for low-frequency-resonance-based piezoelectric devices.20,199,211-214) In addition to the piezoelectric properties, the mechanical quality factor Qm also shows anisotropic behavior, where both high piezoelectric coefficient d33 and mechanical Q33 were observed in the 2R-engineered domain configuration, which will benefit the high-power applications at resonance frequency.20,177,213,215) It is also of interest to point out the other engineered domain configurations, such as the 1O and 3O domain states ([011]- and [111]-poled orthorhombic crystals, respectively). The thickness shear d24 in the 1O single domain state and longitudinal d33 in the 3O domain configuration were reported to be on the order of > 2000 pC/N and > 800 pC/N, respectively, with minimal piezoelectric variation over the studied temperature range; this shows potential for sensor applications (shown in Table 5), where high-temperature stability is demanded.216-218)
From Table 2, we can observe that the 3rd Gen crystals simultaneously possess high coupling and mechanical quality factor, leading to a high FOM of kQm for high-power transducer applications.98,219) In contrast to ceramics, where the coupling is found to decrease with increasing mechanical Q values, the uniqueness of the enhanced mechanical Q values without sacrificing the electromechanical couplings in relaxor-PT single crystals is due to the fact that the coupling is inherently associated with the [001] crystallographic orientation and engineered domain configuration, as shown in Fig. 8.219)
A key signature of relaxor-PT crystals is the existence of PNRs, responsible for the unique high dielectric and piezoelectric properties. The PNRs can behave as “seeds” to facilitate macroscopic polarization rotation and account for 50-80% of their room temperature properties.58,59) Fig. 9(a) gives the transverse dielectric permittivity for single-domain rhombohedral PMN-PT crystals over the temperature range of 25-300 K, exhibiting a relaxor re-entrant behavior at cryogenic temperatures, closely related to the existence of PNRs. The dielectric permittivity was found to be on the order of 700 at 20 K, and jumped to 3200 at 120 K, being the cornerstone for the ultrahigh room-temperature properties. In addition, the thickness shear piezoelectric coefficient was found to follow the same trend as the dielectric permittivity, showing a jump over the same temperature range. Of particular significance is that the value of d15 is still high at 20 K, being on the order of 500 pC/N and comparable to the room-temperature value of its polycrystalline counterpart, as shown in Fig. 9(a). Fig. 9(b) shows the dielectric and piezoelectric properties as a function of temperature for [001]-poled rhombohedral PMN-PT crystals with 4R domain-engineered configuration, where the piezoelectric coefficient d33 is approximately 250 pC/N at 20 K and increased to 1000 pC/N at 100 K.58,59,220,221) This opens a great potential for cryogenic piezoelectric applications; for example, a cryogenic actuator (valve) in cryogenic fluid devices, which can precisely control the flow of liquid gases in various scenarios, such as liquid oxygen and hydrogen for space shuttle propulsion, liquid nitrogen for food freezing, cooling of chamber systems for high-vacuum state, cooling of infrared detector and medical applications, etc.206,220,222-225)
5.2. High-temperature nonferroelectric piezoelectric crystals
Table 7 lists the properties of some actively studied non-ferroelectric piezoelectric crystals for high-temperature piezoelectric applications.7,109,112,122,124,226-229)
Gallium orthophosphate (GaPO4) is the analogue of a-quartz crystal, which shares many of the positive features of quartz, such as high electrical resistivity and mechanical quality factor, while exhibiting higher electromechanical coupling and greater piezoelectric sensitivity at temperatures up to 970°C, where a α-β phase transition occurs.230) Langasite family crystals with the general formula of A3BC3D2O14 were first studied in the 1980s. The structure of langasite La3Ga5SiO14 (LGS), and its isomorphs langatate La3Ga5.5Ta0.5O14 (LGT), however, are disordered, where the large La3+ cations occupy the A sites, and the Ga3+ cations occupy the B, C, and a portion of the D sites, with Si4+ or Ta5+/Nb5+ occupying the remainder of the D sites. Structural disorder can be considered as a type of impurity, leading to phonon scattering and increasing conductivity and mechanical loss at elevated temperatures. Recent developments of LGS-type compounds, based on stringent structural and charge compensation rules, have led to the identification of a group of totally “ordered” langasite-structure crystals, such as Ca3TaGa3Si2O14 (CTGS), in which all the cations were found to be totally ordered, exhibiting greatly improved mechanical Q values and high resistivity at elevated temperatures, but with inferior piezoelectric properties.
Oxyborate crystals with general formula ReCa4O(BO3)3 (Re = rare earth element, abbreviated as ReCOB) was first reported in the 1990s.7) Analogous to langasite crystals, no phase transition(s) occur prior to their melting points, greatly expanding the potential temperature usage range. Recently, oxyborate crystals have attracted extensive attention for high-temperature piezoelectric applications, owing to their ultrahigh electrical resistivity at elevated temperatures, being on the order of 1011 Ω·cm at 500°C for YCOB, greatly expanding their usage at elevated temperatures.112) Owing to the different ionic radii of rare earth cations, ReCOB exhibits property variations, where PrCOB and NdCOB show the highest piezoelectric properties, with d26 being on the order of 15-16 pC/N, while they possess the lowest room-temperature electrical resistivity and mechanical quality factor, being around 1014 Ω·cm and ~ 3800. On the contrary, YCOB and ErCOB crystals were found to possess the lowest effective d26 of 10 pC/N, but with resistivity and mechanical Q values 1017 Ω·cm and ~ 9000.139,226)
Fresnoite crystals with a composition of Ba2TiSi2O8 (BTS) were firstly grown in the 1970s, but this crystal was recently revisited for its high-temperature behavior, owing to the 4 mm symmetry possessing the same piezoelectric matrix as poled ceramics, which make it easier for sensing device design. BTS crystal was found to possess high thickness shear piezoelectric d15 of 17.5 pC/N. Of particular interest is the unique positive extensional piezoelectric d31, in contrast to most piezoelectric materials with 4 mm and 6 mm symmetries, owing to its inherent Poisson’s ratio stress. The positive value of d31 gives rise to a higher longitudinal piezoelectric d33 for (ZXl50°) cut, being on the order of 9.1 pC/N. These good piezoelectric values, together with its high resistivity of 4 × 109 Ω·cm, make it promising for piezoelectric applications at elevated temperatures.124) Another interesting piezoelectric crystal, α-BiB3O6, which was first reported in 1962, was also revisited for its high-temperature piezoelectric properties. This crystal shows high piezoelectric d22 of 40pC/N, but low dielectric ɛ22r of 8.4, leading to a very high piezoelectric voltage coefficient g22, being on the order of 0.538 Vm/N.228,229) The temperature usage range of α-BiB3O6 is limited by its low melting temperature of 726°C.
For high-temperature applications, high insulation resistivity is an important parameter to consider during device operation. For example, in the case of a sensor, the piezoelectric material must not only develop a charge for the applied stress or strain, but must also maintain the charge for a time long enough to be detected by the electronic system. 7) Fig. 10 gives the resistivity as a function of temperature for piezoelectric crystals, where YCOB and GaPO4 are found to possess the highest resistivity, being 3-4 orders higher than those of disordered langasite and ferroelectric lithium niobate crystals. From Table 7, it can be seen that most of the nonferroelectric piezoelectric crystals possess low piezoelectric coefficients << 100 pC/N, and some of them even fall into single digits. Owing to their greatly improved electrical resistivity compared to ferroelectric crystals and the absence of ferroelectric phase transition, they are still found to show potential in piezoelectric sensing applications at elevated temperatures. This has already been demonstrated by many sensing devices at high temperatures,1) such as accelerometers,22,143,190) SAW sensors,142,231) acoustic emission sensors,141) and transducers.191)
In addition to the wide temperature usage range and high resistivity at elevated temperature, the nonferroelectric piezoelectric crystals exhibit ultrahigh temperature stability of the piezoelectric properties. The temperature-dependent coupling factor k26 for various ReCOB crystals is presented in Fig. 11(a). It is found that k26 for PrCOB crystals decreased from 31.5% to 24.7% as the temperature increased from room temperature to 1000°C, giving a variation of −21.6%. Similar trends are observed for GdCOB, SmCOB, NdCOB, and LaCOB crystals, with the variations being on the order of −15% to −27%. Interestingly, the coupling factors k26 for ErCOB and YCOB crystals are found to maintain similar values over the temperature range of 20-1000°C, exhibiting excellent thermal stability. The piezoelectric coefficients d26 are given in Fig. 11(b). The largest d26 value (15.8 pC/N at room temperature) is found for PrCOB crystals, which decreases as the temperature increases to 1000°C, showing a variation of −17%. Relatively low d26 values are determined for ErCOB (7.6 pC/N) and YCOB (7.8 pC/N) crystals, which slightly increased with increasing temperature, exhibiting variations of 20-25% over the temperature range. Of particular significance is that the piezoelectric coefficient (d26) of GdCOB crystals is found to be nearly temperature-independent, being on the order of 11.5 pC/N at room temperature, with less than 5% variation at 1000°C.140)
6. Summary, Challenges, and Perspective
Figure 12 summarizes the sensitivity versus proposed usage temperature range for various piezoelectric materials. It should be noted here that the sensitivity is related to the piezoelectric coefficient or electromechanical coupling factor, based on non-resonance-based applications. For resonance based applications, such as SAW-based SHM sensors, the sensitivity is related to the mechanical quality factor Qm.23) The relaxor-PT ferroelectric single crystals with perovskite structure are found to possess the highest piezoelectric properties, with values being on the order of > 1500 pC/ N. However, the usage temperature range is limited by low ferroelectric phase transition TRTs. Perovskite polycrystalline ceramics, such as PMN-PT, PZT, and BSPT, have sensitivities in the range of 200 pC/N to 900 pC/N, with a usage temperature range of 100-400°C, restricted by thermally activated aging behavior at temperatures far below TCs. Ferroelectric materials with the tungsten bronze structure and Aurivillius structure possess medium piezoelectric properties, ranging from 10 pC/N to 100 pC/N, with usage temperatures up to 550°C, limited by TC or low electrical resistivity at elevated temperature. It should be noted that although LN crystals possess a TC of 1150°C, their low resistivities and oxygen loss at elevated temperature restrict applications to below 600°C. Generally, nonferroelectric piezoelectric single crystals possess low sensitivity, falling in the range of 1-20 pC/N. However, the ultralow dielectric and mechanical losses (high mechanical quality factor Qm), and high electrical resistivities, make them ideal candidates for high-temperature sensing applications. The usage temperature ranges of piezoelectric crystals are limited by the α-β phase transition, melting points, and/or electrical resistivity. In addition, with respect to the ferroelectric polymer materials, despite possessing low piezoelectric coefficient and narrow temperature usage range (depending on their respective glass transition temperature, usually below 60-100°C), their excellent flexibility and ultralow mechanical quality factor find applications for SHM broadband nondestructive ultrasonic testing where it is difficult or impossible to be realized by piezoelectric ceramics or single crystals, on large-area nonplanar structure surfaces.23)
The composite materials, however, combining the advantages of both piezoelectric active materials (high piezoelectric sensitivity) and passive polymer materials (high compliance), are promising candidates for numerous ultrasonic applications. The temperature usage range is determined by the passive polymer, up to 300°C. Of particular significance is that the relaxor-PT-based ferroelectric single crystals were found to still possess high piezoelectric functionality at a cryogenic temperature of −170°C, making them very promising for electromechanical applications at cryogenic temperatures.221)
The application of a piezoelectric material at elevated temperatures presents many challenges, such as phase transitions, which in general lead to temperature-instability of the properties. For example, ferroelectric materials are limited by their respective Curie temperatures TC, above which, the materials will be depolarized and all piezoelectric phenomena are lost. Meanwhile, in piezoelectric single-crystal quartz and gallium orthophosphate, the piezoelectric properties are limited by α-β phase transitions, thus exhibiting discontinuity in the piezoelectric behavior. In devices that operate at low frequencies, electrical conductivity contributes to charge drift interfering with piezoelectrically induced charges. This is a serious issue at elevated temperatures owing to the decreased electrical resistivity, which restricts the applications of many piezoelectric materials to relatively low temperatures or ultrahigh frequency. Additional challenges that piezoelectric materials encounter at elevated temperatures include, but are not limited to: thermal instability of the dielectric, piezoelectric, and electromechanical properties; increased attenuation of acoustic waves and dielectric losses with temperature; chemical instability (decomposition and/or ionic defect creation), which accounts for excessive conductive ions and viscous damping. All these factors must be considered when selecting an appropriate material for a specific high-temperature application. On the contrary, for applications at cryogenic temperatures, the sensitivity and thermal stability of the piezoelectric materials are the key parameters to consider. Generally speaking, the functionality of materials is severely degraded with decreasing temperature. For example, the piezoelectric coefficient of soft PZT is only 50% of its RT value at −150°C. In order to take the full advantage of piezoelectric crystals for different applications over a broad temperature usage range, the dielectric and piezoelectric properties need to be evaluated with respect to temperature, combined with low pO2, vacuum, moisture, and radiation hard conditions. The defect chemistry induced by the harsh environment and its impacts on microstructure and electric properties need to be investigated.
It should be noted that most of the high-performance ferroelectric crystals with perovskite structure are lead-based materials. In response to the legislative activity by the European Union to eliminate toxic substances from electrical and electronic equipment to reduce their negative impact on health and the environment, and to attain the sustainable society development, lead-free piezoelectric materials are in great demand. The resurgence of lead-free piezoelectric material studies occurred in 2004, when Saito et al. reported a high piezoelectric property of ~ 410 pC/N in textured KNN-based ceramics.1,232,233) This development attracted extensive studies on lead-free piezoelectrics, with record values of piezoelectric properties broken frequently. 102,105,234-254) There have been many efforts focusing on the single-crystal growth of lead-free piezoelectrics, including TSSG and SSCG methods,255-272) where the electromechanical coupling factor can reach up to 90%, taking advantage of the engineered domain configuration. However, many challenges exist in the growth and properties of lead-free single crystals, such as volatility of the constituent elements, inhomogeneous components, low quality, small size, low dielectric permittivity and thus low piezoelectric coefficients, low Curie temperature, and low coercive field; all these will limit their applications. Thus, many efforts are required to be focused on the crystal growth and comprehensive understanding of lead-free piezoelectric materials to further increase their piezoelectric properties, taking advantage of the engineered domain configurations, without sacrificing the temperature usage range and field drive stability.
AcknowledgmentsS.Z. acknowledges the support of ONRG under Grant Nos. N62909-16-12126 and N62909-18-12168.
Fig. 1Applications of piezoelectric materials (top-left: medical imaging; top-right: underwater acoustic; bottom-left: SHM of energy plant; bottom-right: SHM of high-temperature engine components; middle: Relaxor-PT ferroelectric crystals (Photo courtesy of TRS Technologies) and nonferroelectric piezoelectric ReCOB crystals (Photo courtesy of Lawrence Livermore National Laboratory and the crystal was grown at Crystal Photonics).5,20,22)

Fig. 11Temperature dependence of electromechanical coupling (left) and piezoelectric (right) for ReCOB single crystals, showing excellent temperature stability.140)
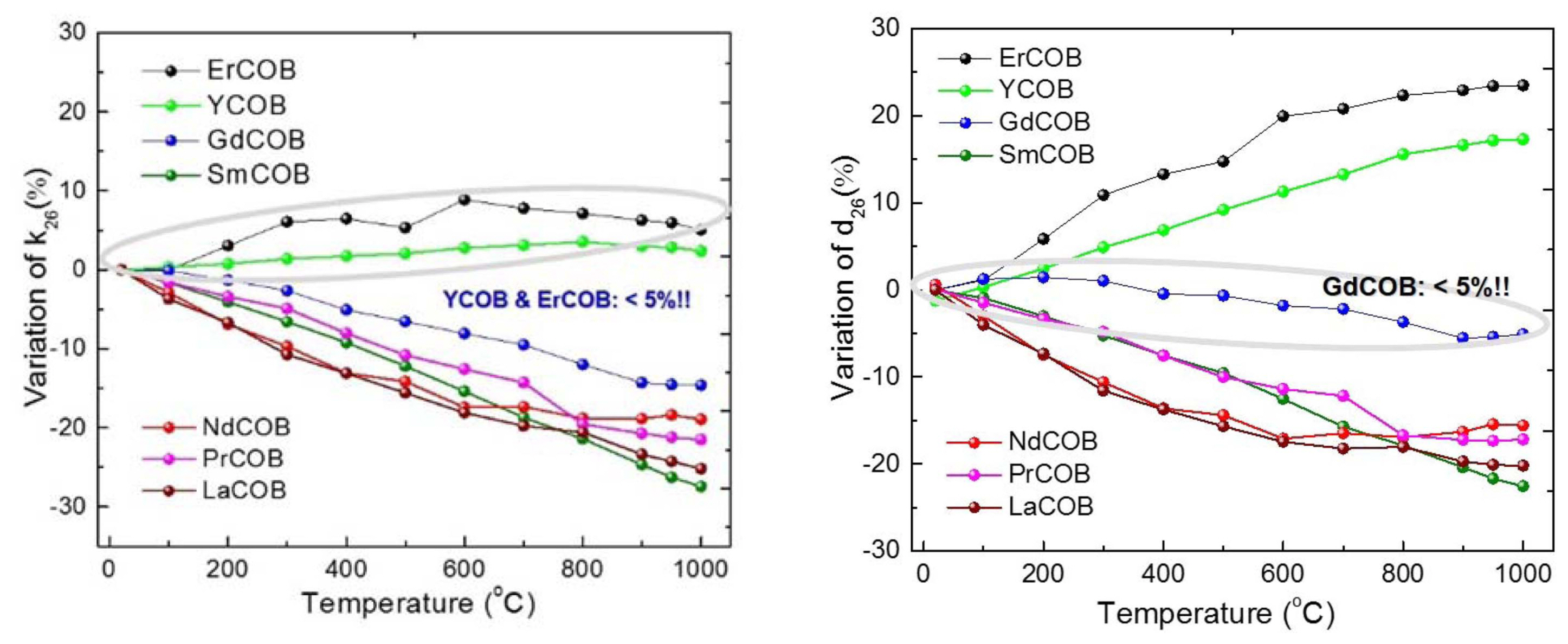
Fig. 12Proposed temperature usage range for various piezoelectric materials, showing different piezoelectric performance (piezoelectric coefficient). (It should be noted that the proposed usage temperature range is based on electrical resistivity for low-frequency sensing applications. For SAW devices, material with low resistivity is still a good choice, such as LN crystals).23) (Structural Health Monitoring (SHM) in Aerospace Structures. Copyright © 2016 Elsevier Ltd.) 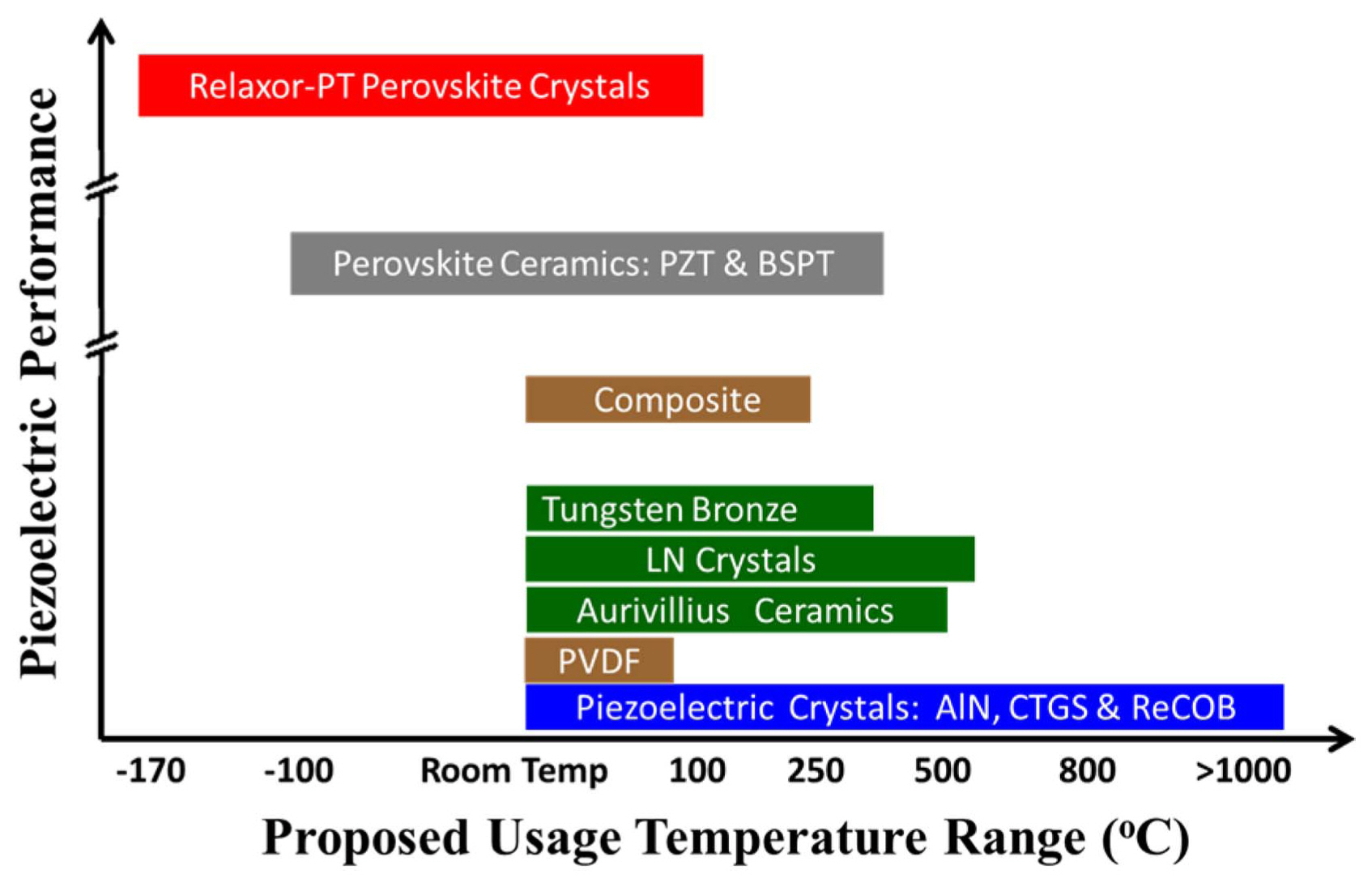
Table 1Key Features of Existing High-Temperature Sensors22)
Table 2Properties of Relaxor-PT Single Crystals with Different Generations in 4R Engineered Domain Configuration
Table 3Property Comparison of Piezoelectric Crystals and Ceramics for Medical Imaging Application Table 4Property Comparison of Piezoelectric Crystals and Ceramics for Actuator Application. d33* (high-field piezoelectric coefficient) is Measured at Electric Field of 20 kV/cm. Table 5Property Comparison of Piezoelectric Crystals and Ceramics for Sensing Application (Temperature stability is measured from −50°C to TO-T, for PZT5A: − 50 ~ 150°C) Table 6Property Comparison of Piezoelectric Crystals and Ceramics for High-Power Transducer Application Table 7
Tuse: the suggested usage temperatures are based on a standard of 1 MΩ·cm resistivity for comparison purposes (apart from LN). Materials with lower resistivity may still be functional in different applications; for example, LN crystals can be used up to 1000°C for short-term and high-frequency (such as SAW) applications.1,198,228) REFERENCES1. S. Trolier-McKinstry, S. Zhang, AJ. Bell, and X. Tan, “High-Performance Piezoelectric Crystals, Ceramics, and Films,” Annu Rev Mater Res, 48 [1] 191-217 (2018).
2. B. Jaffe, R. Roth, and S. Marzullo, “Properties of Piezoelectric Ceramics in the Solid-Solution Series Lead Titanate-Lead Zirconate-Lead Oxide: Tin Oxide and Lead Titanate-Lead Hafnate,” J Res Natl Bur Stand, 55 [5] 239-54 (1955).
3. H. Jaffe, and DA. Berlincourt, “Piezoelectric Transducer Materials,” Proc IEEE, 53 [10] 1372-86 (1965).
4. SE. Park, and TR. Shrout, “Relaxor Based Ferroelectric Single Crystals for Electro-Mechanical Actuators,” Mater Res Innovations, 1 [1] 20-5 (1997).
5. S. Zhang, and F. Li, “High Performance Ferroelectric Relaxor-PbTiO3 Single Crystals: Status and Perspective,” J Appl Phys, 111 [3] 031301(2012).
6. E. Sun, and W. Cao, “Relaxor-Based Ferroelectric Single Crystals: Growth, Domain Engineering, Characterization and Applications,” Prog Mater Sci, 65 124-210 (2014).
7. S. Zhang, F. Yu, and DJ. Green, “Piezoelectric Materials for High Temperature Sensors,” J Am Ceram Soc, 94 [10] 3153-70 (2011).
8. N. Setter, D. Damjanovic, L. Eng, G. Fox, S. Gevorgian, S. Hong, A. Kingon, H. Kohlstedt, NY. Park, GB. Stephenson, I. Stolitchnov, AK. Taganstev, DV. Taylorc, T. Yamada, and S. Streiffer, “Ferroelectric Thin Films: Review of Materials, Properties, and Applications,” J Appl Phys, 100 [5] 051606(2006).
9. D. Damjanovic, “Ferroelectric, Dielectric and Piezoelectric Properties of Ferroelectric Thin Films and Ceramics,” Rep Prog Phys, 61 [9] 1267-324 (1998).
10. S. Trolier-McKinstry, and P. Muralt, “Thin Film Piezoelectrics for MEMS,” J Electroceram, 12 [1-2] 7-17 (2004).
11. GL. Messing, S. Trolier-McKinstry, EM. Sabolsky, C. Duran, S. Kwon, B. Brahmaroutu, P. Park, H. Yilmaz, PW. Rehrig, KB. Eitel, E. Suvaci, M. Seabaugh, and KS. Oh, “Templated Grain Growth of Textured Piezoelectric Ceramics,” Crit Rev Solid State Mater Sci, 29 [2] 45-96 (2004).
12. GL. Messing, S. Poterala, Y. Chang, T. Frueh, ER. Kupp, BH. Watson, RL. Walton, MJ. Brova, A-K. Hofer, R. Bermejo, and RJ. Meyer, “Texture-Engineered Ceramics—Property Enhancements through Crystallographic Tailoring,” J Mater Res, 32 [17] 3219-41 (2017).
13. AJ. Bell, Multilayer Ceramic Processing. pp. 241-71 Ferroelectric Ceramics; In : Setter N, Colla EL, editors, Springer, London, 1993.
14. Q. Li, L. Chen, MR. Gadinski, S. Zhang, G. Zhang, HU. Li, E. Iagodkine, A. Haque, L-Q. Chen, TN. Jackson, and Q. Wang, “Flexible High-Temperature Dielectric Materials from Polymer Nanocomposites,” Nature, 523 [7562] 576-79 (2015).
15. QM. Zhang, V. Bharti, and X. Zhao, “Giant Electrostriction and Relaxor Ferroelectric Behavior in Electron-Irradiated Poly(Vinylidene Fluoride-Trifluoroethylene) Copolymer,” Science, 280 [5372] 2101-5 (1998).
16. RE. Newnham, DP. Skinner, and LE. Cross, “Connectivity and Piezoelectric-Pyroelectric Composites,” Mater Res Bull, 13 [5] 525-36 (1978).
18. WA. Smith, and BA. Auld, “Modeling 1-3 Composite Piezoelectrics: Thickness-Mode Oscillations,” IEEE Trans Ultrason Ferroelectr Freq Control, 38 [1] 40-7 (1991).
19. S. Zhang, F. Li, J. Luo, R. Sahul, and TR. Shrout, “Relaxor-PbTiO3 Single Crystals for Various Applications,” IEEE Trans Ultrason Ferroelectr Freq Control, 60 [8] 1572-80 (2013).
20. S. Zhang, F. Li, X. Jiang, J. Kim, J. Luo, and X. Geng, “Advantages and Challenges of Relaxor-PbTiO3 Ferroelectric Crystals for Electroacoustic Transducers-A Review,” Prog Mater Sci, 68 1-66 (2015).
21. CH. Sherman, “Underwater Sound - A Review I. Underwater Sound Transducers,” IEEE Trans Sonics Ultrason, 22 [5] 281-90 (1975).
22. X. Jiang, K. Kim, S. Zhang, J. Johnson, and G. Salazar, “High-Temperature Piezoelectric Sensing,” Sensors, 14 [1] 144-69 (2013).
23. SJ. Zhang, F. Li, and FP. Yu, Piezoelectric Materials for Cryogenic and High-Temperature Applications. pp. 59-93 Structural Health Monitoring in Aerospace Structures; In : Yuan FG, editor, Woodhead Publishing Limited, Cambridge, 2016.
24. F. Li, S. Zhang, Z. Li, and Z. Xu, “Recent Development on Relaxor-PbTiO3 Single Crystals: The Origin of High Piezoelectric Response,” Prog Phys, 32 178-98 (2012).
25. L. Cross, and R. Newnham, History of Ferroelectrics, Ceramics and Civilation: High Technology Ceramics-Past, Present and Future; 3 pp. 289-305 The American Ceramic Society, 1987.
26. J. Valasek, “Properties of Rochelle Salt Related to the Piezo-Electric Effect,” Phys Rev, 20 [6] 639-64 (1922).
27. D. Berlincourt, and H. Jaffe, “Elastic and Piezoelectric Coefficients of Single-Crystal Barium Titanate,” Phys Rev, 111 [1] 143-48 (1958).
29. GH. Haertling, “Ferroelectric Ceramics: History and Technology,” J Am Ceram Soc, 82 [4] 797-818 (1999).
30. KH. Härdtl, “Electrical and Mechanical Losses in Ferroelectric Ceramics,” Ceram Int, 8 [4] 121-27 (1982).
31. JA. Gallego-Juarez, “Piezoelectric Ceramics and Ultrasonic Transducers,” J Phys E: Sci Instrum, 22 [10] 804-16 (1989).
32. EC. Subbarao, “A Family of Ferroelectric Bismuth Compounds,” J Phys Chem Solids, 23 [6] 665-76 (1962).
33. RE. Newnham, RW. Wolfe, and JF. Dorrian, “Structural Basis of Ferroelectricity in the Bismuth Titanate Family,” Mater Res Bull, 6 [10] 1029-39 (1971).
34. H. Yan, H. Zhang, Z. Zhang, R. Ubic, and MJ. Reece, “B-Site Donor and Acceptor Doped Aurivillius Phase Bi3NbTiO9 Ceramics,” J Eur Ceram Soc, 26 [13] 2785-92 (2006).
35. S. Zhang, N. Kim, TR. Shrout, M. Kimura, and A. Ando, “High Temperature Properties of Manganese Modified CaBi4Ti4O15 Ferroelectric Ceramics,” Solid State Commun, 140 [3-4] 154-58 (2006).
36. H. Hao, H. Liu, and S. Ouyang, “Structure and Ferroelectric Property of Nb-Doped SrBi4Ti4O15 Ceramics,” J Electroceram, 22 [4] 357-62 (2007).
37. C-M. Wang, and J-F. Wang, “Aurivillius Phase Potassium Bismuth Titanate: K0.5Bi4.5Ti4O15
,” J Am Ceram Soc, 91 [3] 918-23 (2008).
38. A. Moure, A. Castro, and L. Pardo, “Aurivillius-Type Ceramics, a Class of High Temperature Piezoelectric Materials: Drawbacks, Advantages and Trends,” Prog Solid State Chem, 37 [1] 15-39 (2009).
39. A. Moure, “Review and Perspectives of Aurivillius Structures as a Lead-Free Piezoelectric System,” Appl Sci, 8 [1] 918-23 (2018).
40. Z-G. Gai, J-F. Wang, M-L. Zhao, C-M. Wang, G-Z. Zang, B-Q. Ming, and P. Qi, “High Temperature (NaBi)0.48□0.04Bi2Nb2O9-Based Piezoelectric Ceramics,” Appl Phys Lett, 89 [1] 012907(2006).
41. C-M. Wang, J-F. Wang, S. Zhang, and TR. Shrout, “Piezoelectric and Electromechanical Properties of Ultrahigh Temperature CaBi2Nb2O9 Ceramics,” Phys Status Solidi RRL, 3 [2-3] 49-51 (2009).
42. T. Yamada, N. Niizeki, and H. Toyoda, “Piezoelectric and Elastic Properties of Lithium Niobate Single Crystals,” Jpn J Appl Phys, 6 [2] 151-55 (1967).
44. FS. Foster, KA. Harasiewicz, and MD. Sherar, “A History of Medical and Biological Imaging with Polyvinylidene Fluoride (PVDF) Transducers,” IEEE Trans Ultrason Ferroelectr Freq Control, 47 [6] 1363-71 (2000).
45. LF. Brown, “Ferroelectric Polymers: Current and Future Ultrasound Applications,” 539-50 (1992).Proceeding Paper?.
46. RE. Newnham, LJ. Bowen, KA. Klicker, and LE. Cross, “Composite Piezoelectric Transducers,” Mater Des, 2 [2] 93-106 (1980).
47. A. Bandyopadhyay, RK. Panda, TF. McNulty, F. Mohammadi, SC. Danforth, and A. Safari, “Piezoelectric Ceramics and Composites via Rapid Prototyping Techniques,” Rapid Prototyping J, 4 [1] 37-49 (1998).
49. F. Li, S. Zhang, D. Damjanovic, LQ. Chen, and TR. Shrout, “Local Structural Heterogeneity and Electromechanical Responses of Ferroelectrics: Learning from Relaxor Ferroelectrics,” Adv Funct Mater, 28 1801504(2018).
50. D. Viehland, SJ. Jang, LE. Cross, and M. Wuttig, “Freezing of the Polarization Fluctuations in Lead Magnesium Niobate Relaxors,” J Appl Phys, 68 [6] 2916-21 (1990).
51. AA. Bokov, BJ. Rodriguez, X. Zhao, J-H. Ko, S. Jesse, X. Long, W. Qu, TH. Kim, JD. Budai, AN. Morozovska, S. Kojima, X. Tan, SV. Kalinin, and Z-G. Ye, “Compositional Disorder, Polar Nanoregions and Dipole Dynamics in Pb(Mg1/3Nb2/3)O3-Based Relaxor Ferroelectrics,” Z Kristallogr, 226 [2] 99-107 (2011).
52. G. Xu, Z. Zhong, Y. Bing, ZG. Ye, and G. Shirane, “Electric-Field-Induced Redistribution of Polar Nano-Regions in a Relaxor Ferroelectric,” Nat Mater, 5 [2] 134-40 (2006).
53. ME. Manley, DL. Abernathy, R. Sahul, DE. Parshall, JW. Lynn, AD. Christianson, PJ. Stonaha, ED. Specht, and JD. Budai, “Giant Electromechanical Coupling of Relaxor Ferroelectrics Controlled by Polar Nanoregion Vibrations,” Sci Adv, 2 [9] e1501814(2016).
54. MA. Carpenter, JF. Bryson, G. Catalan, SJ. Zhang, and NJ. Donnelly, “Elastic and Anelastic Relaxations in the Relaxor Ferroelectric Pb(Mg1/3Nb2/3)O3: II. Strain-Order Parameter Coupling and Dynamic Softening Mechanisms,” J Phys Condens Matter, 24 [4] 045902(2012).
55. J. Macutkevic, J. Banys, A. Bussmann-Holder, and AR. Bishop, “Origin of Polar Nanoregions in Relaxor Ferroelectrics: Nonlinearity, Discrete Breather Formation, and Charge Transfer,” Phys Rev, B, 83 [18] 184301(2011).
56. S-E. Park, and TR. Shrout, “Ultrahigh Strain and Piezoelectric Behavior in Relaxor Based Ferroelectric Single Crystals,” J Appl Phys, 82 [4] 1804-11 (1997).
57. X. Zhao, J. Wang, Z. Peng, KH. Chew, HLW. Chan, CL. Choy, and H. Luo, “Electric Field Effect on Polarization and Depolarization Behavior of the <001>-Oriented Relaxor-Based 0.7Pb(Mg1/3Nb2/3)O3-0.3PbTiO3 Single Crystal,” Phys B, 339 [2-3] 68-73 (2003).
58. F. Li, S. Zhang, T. Yang, Z. Xu, N. Zhang, G. Liu, J. Wang, J. Wang, Z. Cheng, Z-G. Ye, J. Luo, TR. Shrout, and L-Q. Chen, “The Origin of Ultrahigh Piezoelectricity in Relaxor-Ferroelectric Solid Solution Crystals,” Nat Commun, 7 13807(2016).
59. F. Li, S. Zhang, Z. Xu, and L-Q. Chen, “The Contributions of Polar Nanoregions to the Dielectric and Piezoelectric Responses in Domain-Engineered Relaxor-PbTiO3 Crystals,” Adv Funct Mater, 27 [18] 1700310(2017).
60. F. Li, D. Lin, Z. Chen, Z. Cheng, J. Wang, C. Li, Z. Xu, Q. Huang, X. Liao, L-Q. Chen, TR. Shrout, and S. Zhang, “Ultrahigh Piezoelectricity in Ferroelectric Ceramics by Design,” Nat Mater, 17 [4] 349-54 (2018).
61. A. Biancoli, CM. Fancher, JL. Jones, and D. Damjanovic, “Breaking of Macroscopic Centric Symmetry in Paraelectric Phases of Ferroelectric Materials and Implications for Flexoelectricity,” Nat Mater, 14 [2] 224-29 (2015).
62. D. Damjanovic, “Piezoelectric Properties of Perovskite Ferroelectrics: Unsolved Problems and Future Research,” Annales de Chimie Science des Matériaux, 26 [1] 99-106 (2001).
63. D. Damjanovic, “Contributions to the Piezoelectric Effect in Ferroelectric Single Crystals and Ceramics,” J Am Ceram Soc, 88 [10] 2663-76 (2005).
64. M. Ahart, A. Asthagiri, Z-G. Ye, P. Dera, H-K. Mao, RE. Cohen, and RJ. Hemley, “Brillouin Scattering and Molecular Dynamics Study of the Elastic Properties of Pb(Mg1/3Nb2/3)O3
,” Phys Rev B, 75 [14] 144410(2007).
65. HY. Guo, C. Lei, and Z-G. Ye, “Re-Entrant Type Relaxor Behavior in (1-x)BaTiO3-xBiScO3 Solid Solution,” Appl Phys Lett, 92 [17] 172901(2008).
66. M. Saidul Islam, S. Tsukada, W. Chen, Z-G. Ye, and S. Kojima, “Role of Dynamic Polar Nanoregions in Heterovalent Perovskite Relaxor: Inelastic Light Scattering Study of Ferroelectric Ti Rich Pb(Zn1/3Nb2/3)O3-PbTiO3
,” J Appl Phys, 112 [11] -114106 (2012).
67. AA. Bokov, and Z-G. Ye, Reentrant Phenomena in Relaxors. pp. 729-64 Nanoscale Ferroelectrics and Multiferroics: Key Processing and Characterization Issues, and Nanoscale Effects; I & II In : Algueró M, Gregg JM, Mitoseriu L, editors, John Wiley & Sons, Chichester, 2016.
68. MJ. Cabral, S. Zhang, EC. Dickey, and JM. LeBeau, “Gradient Chemical Order in the Relaxor Pb(Mg1/3Nb2/3)O3
,” Appl Phys Lett, 112 [8] 082901(2018).
69. TR. Shrout, and J. Fielding, “Relaxor Ferroelectric Materials,” pp. 711-20 In: Proceedings of IEEE Symposium on Ultrasonics; 1990.
70. YH. Bing, and ZG. Ye, “Effects of Chemical Compositions on the Growth of Relaxor Ferroelectric Pb(Sc1/2Nb1/2)1-xTixO3 Single Crystals,” J Cryst Growth, 250 [1-2] 118-25 (2003).
71. S. Zhang, L. Laurent, S. Rhee, CA. Randall, and TR. Shrout, “Shear-Mode Piezoelectric Properties of Pb(Yb1/2Nb1/2)O3-PbTiO3 Single Crystals,” Appl Phys Lett, 81 [5] 892-94 (2002).
72. N. Yasuda, H. Ohwa, M. Kume, Y. Hosono, Y. Yamashita, S. Ishino, H. Terauchi, M. Iwata, and Y. Ishibashi, “Crystal Growth and Dielectric Properties of Solid Solutions of Pb(Yb1/2Nb1/2)O3-PbTiO3 with a High Curie Temperature near a Morphotropic Phase Boundary,” Jpn J Appl Phys, 40 [Part 1, No. 9B] 5664-67 (2001).
73. N. Yasuda, M. Sakaguchi, Y. Itoh, H. Ohwa, Y. Yamashita, M. Iwata, and Y. Ishibashi, “Effect of Electric Fields on Domain Structure and Dielectric Properties of Pb(In1/2Nb1/2)O3-PbTiO3 near Morphotropic Phase Boundary,” Jpn J Appl Phys, 42 [Part 1, No. 9B] 6205-8 (2003).
74. Y. Guo, H. Luo, T. He, and Z. Yin, “Peculiar Properties of a High Curie Temperature Pb(In1/2Nb1/2)O3-PbTiO3 Single Crystal Grown by the Modified Bridgman Technique,” Solid State Commun, 123 [9] 417-20 (2002).
75. S. Zhang, CA. Randall, and TR. Shrout, “High Curie Temperature Piezocrystals in the BiScO3-PbTiO3 Perovskite System,” Appl Phys Lett, 83 [15] 3150-52 (2003).
76. S. Zhang, L. Lebrun, S. Rhee, RE. Eitel, CA. Randall, and TR. Shrout, “Crystal Growth and Characterization of New High Curie Temperature (1-x)BiScO3-xPbTiO3 Single Crystals,” J Cryst Growth, 236 [1-3] 210-16 (2002).
77. Y. Hosono, Y. Yamashita, H. Sakamoto, and N. Ichinose, “Growth of Single Crystals of High-Curie-Temperature Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Ternary Systems near Morphotropic Phase Boundary,” Jpn J Appl Phys, 42 [Part 1, No. 9A] 5681-86 (2003).
78. N. Yasuda, T. Fuwa, H. Ohwa, Y. Tachi, Y. Yamashita, K. Fujita, M. Iwata, H. Terauchi, and Y. Ishibashi, “Hierarchical Domain Structures in Relaxor 24Pb(In1/2Nb1/2)O3-46Pb(Mg1/3Nb2/3)O3-30PbTiO3 near a Morphotropic Phase Boundary Composition Grown by Bridgman Method,” Jpn J Appl Phys, 50 [9S2] 09NC1(2011).
79. S. Zhang, J. Luo, W. Hackenberger, and TR. Shrout, “Characterization of Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Ferroelectric Crystal with Enhanced Phase Transition Temperatures,” J Appl Phys, 104 [6] 064106(2008).
80. X. Liu, S. Zhang, J. Luo, TR. Shrout, and W. Cao, “Complete Set of Material Constants of Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 Single Crystal with Morphotropic Phase Boundary Composition,” J Appl Phys, 106 [7] 074112(2009).
81. X. Liu, S. Zhang, J. Luo, TR. Shrout, and W. Cao, “A Complete Set of Material Properties of Single Domain 0.26Pb(In1/2Nb1/2)O3-0.46Pb(Mg1/3Nb2/3)O3-0.28PbTiO3 Single Crystals,” Appl Phys Lett, 96 [1] 012907(2010).
82. S. Zhang, J. Luo, W. Hackenberger, NP. Sherlock, RJ. Meyer Jr, and TR. Shrout, “Electromechanical Characterization of [Formula: See Text] Crystals as a Function of Crystallographic Orientation and Temperature,” J Appl Phys, 105 [10] 104506(2009).
83. X. Li, and H. Luo, “The Growth and Properties of Relaxor-Based Ferroelectric Single Crystals,” J Am Ceram Soc, 93 [10] 2915-28 (2010).
84. Y. Zhang, DA. Liu, Q. Zhang, W. Wang, B. Ren, X. Zhao, and H. Luo, “Complete Set of Material Constants of <011>-Poled Rhombohedral Single-Crystal 0.25Pb(In1/2Nb1/2)O3-0.47Pb(Mg1/3Nb2/3)O3-0.28PbTiO3
,” J Electron Mater, 40 [1] 92-6 (2010).
85. Y. Wang, Z. Wang, W. Ge, C. Luo, J. Li, D. Viehland, J. Chen, and H. Luo, “Temperature-Induced and Electric-Field-Induced Phase Transitions in Rhombohedral Pb(In1/2Nb1/2)O3 -Pb(Mg1/3Nb2/3)O3-PbTiO3 Ternary Single Crystals,” Phys Rev B, 90 [13] 134107(2014).
86. N. Hidayah, N. Yasuda, H. Ohwa, Y. Tachi, Y. Yamashita, and M. Iwata, “Poling and Depoling Effects on Dielectric Properties and Domain Structures in Relaxor 24Pb(In1/2Nb1/2)O3 -46Pb(Mg1/3Nb2/3)O3-30PbTiO3 near a Morphotropic Phase Boundary Composition,” Jpn J Appl Phys, 51 [9S1] 09LC6(2012).
87. J. Luo, and S. Zhang, “Advances in the Growth and Characterization of Relaxor-PT-Based Ferroelectric Single Crystals,” Crystals, 4 [3] 306-30 (2014).
88. D. Carka, J. Gallagher, and C. Lynch, “Phase Energy Determined from Stress and Electric-Field-Induced Phase Transformations in [011]C Cut 0.24PIN-PMN-PT Single Crystals,” Crystals, 4 [3] 377-89 (2014).
89. W. He, Q. Li, Q. Yan, N. Luo, Y. Zhang, X. Chu, and D. Shen, “Temperature-Dependent Phase Transition in Orthorhombic [011]c Pb(Mg1/3Nb2/3)O3-0.35PbTiO3 Single Crystal,” Crystals, 4 [3] 262-72 (2014).
90. F. Li, S. Zhang, D. Lin, J. Luo, Z. Xu, X. Wei, J. Luo, and TR. Shrout, “Electromechanical Properties of Pb(In12Nb12)O3-Pb(Mg13Nb23)O3-PbTiO3 Single Crystals,” J Appl Phys, 109 [1] 014108(2011).
91. J. Tian, and P. Han, “Growth and Characterization on PMN-PT-Based Single Crystals,” Crystals, 4 [3] 331-41 (2014).
92. X. Jiang, J. Kim, and K. Kim, “Relaxor-PT Single Crystal Piezoelectric Sensors,” Crystals, 4 [3] 351-76 (2014).
93. S. Zhang, SM. Lee, DH. Kim, HY. Lee, and TR. Shrout, “Characterization of High TC Pb(Mg1/3Nb2/3)O3-PbZrO3-PbTiO3 Single Crystals Fabricated by Solid State Crystal Growth,” Appl Phys Lett, 90 [23] 232911(2007).
94. S. Zhang, S-M. Lee, D-H. Kim, H-Y. Lee, and TR. Shrout, “Electromechanical Properties of PMN-PZT Piezoelectric Single Crystals Near Morphotropic Phase Boundary Compositions,” J Am Ceram Soc, 90 [12] 3859-62 (2007).
95. A. Amin, H-Y. Lee, and B. Kelly, “High Transition Temperature Lead Magnesium Niobate-Lead Zirconate Titanate Single Crystals,” Appl Phys Lett, 90 [24] 242912(2007).
96. T. Richter, C. Schuh, E. Suvaci, and R. Moos, “Single Crystal Growth in PMN-PT and PMN-PZT,” J Mater Sci, 44 [7] 1757-63 (2009).
97. Z. Xia, and Q. Li, “Growth and Characterization of Pb(Mg1/3Nb2/3)O3-PbTiO3-PbZrO3 Single Crystals with High Rhombohedral/Tetragonal Phase Transition Temperature,” Solid State Commun, 145 [1-2] 38-42 (2008).
98. S. Zhang, SM. Lee, DH. Kim, HY. Lee, and TR. Shrout, “Characterization of Mn-Modified Pb(Mg1/3Nb2/3)O3-PbZrO3-PbTiO3 Single Crystals for High Power Broad Bandwidth Transducers,” Appl Phys Lett, 93 [12] 122908(2008).
99. AJ. Bell, “A Classical Mechanics Model for the Interpretation of Piezoelectric Property Data,” J Appl Phys, 118 [22] 224103(2015).
100. AJ. Bell, “Phenomenologically Derived Electric Field-Temperature Phase Diagrams and Piezoelectric Coefficients for Single Crystal Barium Titanate under Fields along Different Axes,” J Appl Phys, 89 [7] 3907-14 (2001).
101. AJ. Bell, “Factors Influencing the Piezoelectric Behaviour of PZT and other “Morphotropic Phase Boundary” Ferroelectrics,” J Mater Sci, 41 [1] 13-25 (2006).
102. TR. Shrout, and SJ. Zhang, “Lead-Free Piezoelectric Ceramics: Alternatives for PZT?,” J Electroceram, 19 [1] 113-26 (2007).
103. Y. Dai, X. Zhang, and G. Zhou, “Phase Transitional Behavior in K0.5Na0.5NbO3-LiTaO3 Ceramics,” Appl Phys Lett, 90 [26] 262903(2007).
104. W. Liu, and X. Ren, “Large Piezoelectric Effect in Pb-Free Ceramics,” Phys Rev Lett, 103 [25] 257602(2009).
105. M. Acosta, N. Novak, V. Rojas, S. Patel, R. Vaish, J. Koruza, GA. Rossetti Jr, and J. Rödel1, “BaTiO3-Based Piezoelectrics: Fundamentals, Current Status, and Perspectives,” Appl Phys Rev, 4 [4] 041305(2017).
106. H. Fritze, “High-Temperature Piezoelectric Crystals and Devices,” J Electroceram, 26 [1-4] 122-61 (2011).
107. WM. Kriven, JW. Palko, S. Sinogeikin, JD. Bass, A. Sayir, G. Brunauer, H. Boysen, F. Frey, and J. Schneider, “High Temperature Single Crystal Properties of Mullite,” J Eur Ceram Soc, 19 [13-14] 2529-41 (1999).
108. BR. Tittmann, and M. Aslan, “Ultrasonic Sensors for High Temperature Applications,” Jpn J Appl Phys, 38 [Part 1, No. 5B] 3011-13 (1999).
109. S. Zhang, Y. Zheng, H. Kong, J. Xin, E. Frantz, and TR. Shrout, “Characterization of High Temperature Piezoelectric Crystals with an Ordered Langasite Structure,” J Appl Phys, 105 [11] 114107(2009).
110. H. Fritze, HL. Tuller, G. Borchardt, and T. Fukuda, “High-Temperature Properties of Langasite,” 65-70 Proceedings of Material Research Symposium, 604 (2000).
111. H. Takeda, M. Hagiwara, H. Noguchi, T. Hoshina, T. Takahashi, N. Kodama, and T. Tsurumi, “Calcium Aluminate Silicate Ca2Al2SiO7 Single Crystal Applicable to Piezoelectric Sensors at High Temperature,” Appl Phys Lett, 102 [24] 242907(2013).
112. F. Yu, S. Hou, X. Zhao, and S. Zhang, “High-Temperature Piezoelectric Crystals ReCa4O(BO3)3: a Review,” IEEE Trans Ultrason Ferroelectr Freq Control, 61 [8] 1344-56 (2014).
113. T. Kim, J. Kim, R. Dalmau, R. Schlesser, E. Preble, and X. Jiang, “High-Temperature Electromechanical Characterization of AlN Single Crystals,” IEEE Trans Ultrason Ferroelectr Freq Control, 62 [10] 1880-87 (2015).
114. P. Krempl, G. Schleinzer, and W. Wallnöfer, “Gallium Phosphate, GaPO4: a New Piezoelectric Crystal Material for High-Temperature Sensorics,” Sens Actuators, A, 61 [1-3] 361-63 (1997).
115. I. Mateescu, F. Krispel, S. Georgescu, K. Scott, and E. Borca, “Comparative Study of the Mass-Loading Effect on Electrical Parameters of Gallium Phosphate, Quartz and Langasite Resonators,” pp. 690-94 In: Proceedings of IEEE International Frequency Control Symposium; 2007.
116. C. Caliendo, and F. Castro, “Quasi-Linear Polarized Modes in Y-Rotated Piezoelectric GaPO4 Plates,” Crystals, 4 [3] 228-40 (2014).
117. P. Armand, A. Lignie, M. Beaurain, and P. Papet, “Flux-Grown Piezoelectric Materials: Application to α-Quartz Analogues,” Crystals, 4 [2] 168-89 (2014).
118. P. Armand, M. Beaurain, B. Ruffle, B. Menaert, D. Balitsky, S. Clement, and P. Papet, “Characterizations of Piezoelectric GaPO4 Single Crystals Grown by the Flux Method,” J Cryst Growth, 310 [7-9] 1455-59 (2008).
119. M. Beaurain, P. Armand, D. Balitsky, P. Papet, and J. Detaint, “Physical Characterizations of α-GaPO4 Single Crystals Grown by the Flux Method,” pp. 1077-81 In: Proceedings of IEEE International Frequency Control Symposium; 2007.
120. W. Soluch, R. Ksiezopolski, W. Piekarczyk, M. Berkowski, MA. Goodberlet, and JF. Vetelino, “Elastic, Piezoelectric, and Dielectric Properties of the BaLaGa3O7 Crystal,” J Appl Phys, 58 [6] 2285-87 (1985).
121. C. Shen, S. Zhang, W. Cao, H. Cong, H. Yu, J. Wang, and H. Zhang, “Thermal and Electromechanical Properties of Melilite-Type Piezoelectric Single Crystals,” J Appl Phys, 117 [6] 064106(2015).
122. C. Shen, H. Zhang, Y. Zhang, H. Xu, H. Yu, J. Wang, and S. Zhang, “Orientation and Temperature Dependence of Piezoelectric Properties for Sillenite-Type Bi12TiO20 and Bi12SiO20 Single Crystals,” Crystals, 4 [2] 141-51 (2014).
123. H. Yamauchi, “Surface-Acoustic-Wave Characteristics on Fresnoite (Ba2Si2TiO8) Single Crystal,” J Appl Phys, 49 [12] 6162-64 (1978).
124. C. Shen, H. Zhang, H. Cong, H. Yu, J. Wang, and S. Zhang, “Investigations on the Thermal and Piezoelectric Properties of Fresnoite Ba2TiSi2O8 Single Crystals,” J Appl Phys, 116 [4] 044106(2014).
125. M. Kimura, K. Doi, S. Nanamatsu, and T. Kawamura, “A New Piezoelectric Crystal: Ba2Ge2TiO8
,” Appl Phys Lett, 23 [10] 531-32 (1973).
126. H. Takeda, T. Kuze, T. Nishida, K. Uchiyama, and T. Shiosaki, “Growth and Piezoelectric Properties of Al-Substituted Langasite-Type La3Nb0.5Ga5.5O14 Crystals,” Mater Res Bull, 43 [7] 1731-36 (2008).
127. YV. Pisarevsky, P. Senushencov, P. Popov, and B. Mill, “New Strong Piezoelectric La3Ga5.5Nb0.5O14 with Temperature Compensation Cuts,” pp. 653-56 In: Proceedings of IEEE International Frequency Control Symposium; 1995.
128. T. Fukuda, P. Takeda, K. Shimamura, H. Kawanaka, M. Kumatoriya, S. Murakami, J. Sato, and M. Sato, “Growth of New Langasite Single Crystals for Piezoelectric Applications,” pp. 315-19 In: Proceedings of the IEEE International Symposium on Applications of Ferroelectrics; 1998.
129. J. Bohm, RB. Heimann, M. Hengst, R. Roewer, and J. Schindler, “Czochralski Growth and Characterization of Piezoelectric Single Crystals with Langasite Structure: La3Ga5SiO14 (LGS), La3Ga5.5Nb0.5O14 (LGN), and La3Ga5.5Ta0.5O14 (LGT): Part I,” J Cryst Growth, 204 [1-2] 128-36 (1999).
130. BHT. Chai, ANP. Bustamante, and MC. Chou, “A new class of ordered langasite structure compounds,” pp. 163-68 In: Proceeding of IEEE/EIA International Frequency Control Symposium; 2000.
131. BV. Mill, and YV. Pisarevsky, “Langasite-type materials: from discovery to present state,” pp. 133-44 In: Proceeding of IEEE/EIA International Frequency Control Symposium; 2000.
132. H. Fritze, M. Schulz, H. Seh, and H. Tuller, “Sensor Application-Related Defect Chemistry and Electromechanical Properties of Langasite,” Solid State Ionics, 177 [26-32] 2313-16 (2006).
133. F. Yu, X. Zhao, L. Pan, F. Li, D. Yuan, and S. Zhang, “Investigation of Zero Temperature Compensated Cuts in Langasite-Type Piezocrystals for High Temperature Applications,” J Phys D: Appl Phys, 43 [16] 165402(2010).
134. J. Xin, Y. Zheng, H. Kong, H. Chen, X. Tu, and E. Shi, “Growth of a New Ordered Langasite Structure Crystal Ca3TaAl3Si2O14
,” Cryst Growth Des, 8 [8] 2617-19 (2008).
135. S. Zhang, H. Kong, R. Xia, Y. Zheng, J. Xin, and TR. Shrout, “Growth and High-Temperature Electromechanical Properties of (and Al) Piezoelectric Crystals,” Solid State Commun, 150 [9-10] 435-38 (2010).
136. K. Xiong, Y. Zheng, X. Tu, S. Zhang, H. Kong, and E. Shi, “Growth and High Temperature Properties of Ca3Ta(Al0.9Ga0.1)3Si2O14 Crystals with Ordered Langasite Structure,” J Cryst Growth, 401 820-23 (2014).
137. S. Zhang, E. Frantz, R. Xia, W. Everson, J. Randi, DW. Snyder, and TR. Shrout, “Gadolinium Calcium Oxyborate Piezoelectric Single Crystals for Ultrahigh Temperature (> 1000°C) Applications,” J Appl Phys, 104 [8] 084103(2008).
138. H. Shimizu, T. Nishida, H. Takeda, and T. Shiosaki, “Dielectric, Elastic and Piezoelectric Properties of RCa4O(BO3)3 (R=Rare-Earth Elements) Crystals with Monoclinic Structure of Point Group m,” J Cryst Growth, 311 [3] 916-20 (2009).
139. F. Yu, S. Zhang, X. Zhao, D. Yuan, C-M. Wang, and TR. Shrout, “Characterization of Neodymium Calcium Oxyborate Piezoelectric Crystal with Monoclinic Phase,” Cryst Growth Des, 10 [4] 1871-77 (2010).
140. F. Yu, S. Zhang, X. Zhao, D. Yuan, L. Qin, QM. Wang, and TR. Shrout, “Dielectric and Electromechanical Properties of Rare Earth Calcium Oxyborate Piezoelectric Crystals at High Temperatures,” IEEE Trans Ultrason Ferroelectr Freq Control, 58 [4] 868-73 (2011).
141. JA. Johnson, K. Kim, S. Zhang, D. Wu, and X. Jiang, “High-Temperature Acoustic Emission Sensing Tests Using a Yttrium Calcium Oxyborate Sensor,” IEEE Trans Ultrason Ferroelectr Freq Control, 61 [5] 805-14 (2014).
142. H. Zu, H. Wu, and QM. Wang, “High-Temperature Piezoelectric Crystals for Acoustic Wave Sensor Applications,” IEEE Trans Ultrason Ferroelectr Freq Control, 63 [3] 486-505 (2016).
143. S. Zhang, X. Jiang, M. Lapsley, P. Moses, and TR. Shrout, “Piezoelectric Accelerometers for Ultrahigh Temperature Application,” Appl Phys Lett, 96 [1] 013506(2010).
144. D. Yuan, Z. Jia, J. Wang, Z. Gao, J. Zhang, X. Fu, J. Shu, Y. Yin, Q. Hua, and X. Tao, “Bulk Growth, Structure, and Characterization of the New Monoclinic TbCa4O(BO3)3 Crystal,” CrystEngComm, 16 [19] 4008-15 (2014).
145. VG. Smotrakov, VV. Eremkin, AE. Panich, LA. Shilkina, and VA. Aleshin, “Optimization of Ceramic Fillers for 0-3 Piezoelectric Composites,” Inorg Mater, 40 [7] 780-83 (2004).
146. SJ. Krumbein, “Metallic Electromigration Phenomena,” IEEE Trans Compon, Hybrids, Manuf Technol, 11 [1] 5-15 (1988).
147. X. Long, and Z-G. Ye, “Top-Seeded Solution Growth and Characterization of Rhombohedral PMN-30PT Piezoelectric Single Crystals,” Acta Mater, 55 [19] 6507-12 (2007).
148. D. Pang, X. Long, and H. Tailor, “A Lead-Reduced Ferrolectric Solid Solution with High Curie Temperature: BiScO3-Pb(Zn1/3Nb2/3)O3-PbTiO3
,” Ceram Int, 40 [8] 12953-59 (2014).
149. C. He, X. Li, Z. Wang, Y. Liu, D. Shen, T. Li, and X. Long, “Characterization of Pb(In1/2Nb1/2)O3-PbTiO3 Ferroelectric Crystals Grown by Top-Seeded Solution Growth Method,” J Alloys Compd, 539 17-20 (2012).
150. T. Li, and X. Long, “High-Performance Ferroelectric Solid Solution Crystals: Pb(In1/2Nb1/2)O3-Pb(Zn1/3Nb2/3)O3-PbTiO3
,” J Am Ceram Soc, 97 [9] 2850-57 (2014).
151. M. Matsushita, Y. Tachi, and K. Echizenya, “Growth of 3- in Single Crystals of Piezoelectric Pb[(Zn1/3Nb2/3)0.91Ti0.09]O3 by the Supported Solution Bridgman Method,” J Cryst Growth, 237-239 853-57 (2002).
152. J. Xu, J. Tong, M. Shi, A. Wu, and S. Fan, “Flux Bridgman growth of Pb[(Zn1/3Nb2/3)0.93Ti0.07]O3 Piezocrystals,” J Cryst Growth, 253 [1-4] 274-79 (2003).
153. LC. Lim, and KK. Rajan, “High-Homogeneity High-Performance Flux-Grown Pb(Zn1/3Nb2/3)O3-(6-7)%PbTiO3 Single Crystals,” J Cryst Growth, 271 [3-4] 435-44 (2004).
154. M. Jin, J. Xu, M. Shi, X. Wu, and J. Tong, “Growth of High Performance Piezoelectric Crystal Pb(Zn1/3Nb2/3)O3-PbTiO3 Using PbO Flux,” Ultrasonics, 46 [2] 129-32 (2007).
155. S. Zhang, L. Laurent, S. Liu, S. Rhee, CA. Randall, and TR. Shrout, “Piezoelectric Shear Coefficients of Pb(Zn1/3Nb2/3)O3-PbTiO3 Single Crystals,” Jpn J Appl Phys, 41 [Part 2, No. 10A] L1099-102 (2002).
156. J. Xu, S. Fan, B. Lu, J. Tong, and A. Zhang, “Seeded Growth of Relaxor Ferroelectric Single Crystals Pb[(Zn1/3Nb2/3)0.91Ti0.09]O3 by the Vertical Bridgman Method,” Jpn J Appl Phys, 41 [Part 1, No. 11B] 7000-2 (2002).
157. J. Xu, X. Wu, J. Tong, M. Shi, and G. Qian, “Two-Step Bridgman Growth of 0.91Pb(Zn1/3Nb2/3)O3-0.09PbTiO3 Single Crystals,” J Cryst Growth, 280 [1-2] 107-12 (2005).
158. KK. Rajan, YS. Ng, J. Zhang, and LC. Lim, “[001]-Poled Pb(Zn1/3Nb2/3)O3-(6-7)%PbTiO3
k
31-Actuators: Effects of Initial Domain Structure, Length Orientation, and Poling Conditions,” Appl Phys Lett, 85 [18] 4136-38 (2004).
159. S-JL. Kang, J-H. Park, S-Y. Ko, H-Y. Lee, and DJ. Green, “Solid-State Conversion of Single Crystals: The Principle and the State-of-the-Art,” J Am Ceram Soc, 98 [2] 347-60 (2015).
160. H-Y. Lee, J-S. Kim, and D-Y. Kim, “Fabrication of BaTiO3 Single Crystals Using Secondary Abnormal Grain Growth,” J Eur Ceram Soc, 20 [10] 1595-97 (2000).
161. M-S. Kim, JG. Fisher, S-JL. Kang, and H-Y. Lee, “Grain Growth Control and Solid-State Crystal Growth by Li2O/PbO Addition and Dislocation Introduction in the PMN-35PT System,” J Am Ceram Soc, 89 [4] 1237-43 (2006).
162. A. Amin, LE. Cross, and H-Y. Lee, “Evolution of a Non-spontaneous, High Piezoelectric Coupling Symmetry Axis in Relaxor-Ferroelectric Single Crystals,” J Appl Phys, 101 [11] 114103(2007).
163. K-S. Moon, D. Rout, H-Y. Lee, and S-JL. Kang, “Solid State Growth of Na1/2Bi1/2TiO3-BaTiO3 Single Crystals and Their Enhanced Piezoelectric Properties,” J Cryst Growth, 317 [1] 28-31 (2011).
164. JB. Lim, S. Zhang, H-Y. Lee, and TR. Shrout, “Solid State Crystal Growth of BiScO3-Pb(Mg1/3Nb2/3)O3-PbTiO3
,” J Electroceram, 29 [2] 139-43 (2012).
165. J-H. Park, H-Y. Lee, and S-JL. Kang, “Solid-State Conversion of (Na1/2Bi1/2)TiO3-BaTiO3-(K1/2Na1/2)NbO3 Single Crystals and Their Piezoelectric Properties,” Appl Phys Lett, 104 [22] 222910(2014).
166. J-Y. Lee, H-T. Oh, and H-Y. Lee, “Dielectric and Piezoelectric Properties of “Lead-Free” Piezoelectric Rhombohedral Ba(Ti0.92Zr0.08)O3 Single Crystals,” J Korean Ceram Soc, 53 [2] 171-77 (2016).
167. H-T. Oh, J-Y. Lee, and H-Y. Lee, “Mn-Modified PMN-PZT [Pb(Mg1/3Nb2/3)O3-Pb(Zr,Ti)O3] Single Crystals for High Power Piezoelectric Transducers,” J Korean Ceram Soc, 54 [2] 150-57 (2017).
168. H-T. Oh, H-J. Joo, M-C. Kim, and H-Y. Lee, “Thickness-Dependent Properties of Undoped and Mn-doped (001) PMN-29PT [Pb(Mg1/3Nb2/3)O3-29PbTiO3] Single Crystals,” J Korean Ceram Soc, 55 [3] 290-98 (2018).
169. J. Callerame, RH. Tancrell, and DT. Wilson, “Transmitters and Receivers for Medical Ultrasonics,” pp. 407-11 In: Proceeding of IEEE Ultrasonics Symposium; 1979.
170. Z. Zhang, F. Li, R. Chen, T. Zhang, X. Cao, S. Zhang, Thomas R. Shrout, Hairong. Zheng, K. Kirk Shung, Mark S. Humayun, Weibao. Qiu, and Qifa. Zhou, “High-Performance Ultrasound Needle Transducer Based on Modified PMN-PT Ceramic With Ultrahigh Clamped Dielectric Permittivity,” IEEE Trans Ultrason Ferroelectr Freq Control, 65 [2] 223-30 (2018).
171. NP. Sherlock, LM. Garten, SJ. Zhang, TR. Shrout, and RJ. Meyer, “Nonlinear Dielectric Response in Piezoelectric Materials for Underwater Transducers,” J Appl Phys, 112 [12] 124108(2012).
172. S. Trolier-McKinstry, N. Bassiri Gharb, and D. Damjanovic, “Piezoelectric Nonlinearity due to Motion of 180° Domain Walls in Ferroelectric Materials at Subcoercive Fields: A Dynamic Poling Model,” Appl Phys Lett, 88 [20] 202901(2006).
173. A. Bernal, S. Zhang, and N. Bassiri-Gharb, “Effects of Orientation and Composition on the Extrinsic Contributions to the Dielectric Response of Relaxor-Ferroelectric Single Crystals,” Appl Phys Lett, 95 [14] 142911(2009).
174. NP. Sherlock, and RJ. Meyer, “Large Signal Response and Harmonic Distortion in Piezoelectrics for SONAR Transducers,” J Electroceram, 28 [2-3] 202-7 (2012).
175. NP. Sherlock, and RJ. Meyer Jr, “Modified Single Crystals for High-Power Underwater Projectors,” IEEE Trans Ultrason Ferroelectr Freq Control, 59 [6] 1285-91 (2012).
176. NP. Sherlock, S. Zhang, J. Luo, H-Y. Lee, TR. Shrout, and RJ. Meyer, “Large Signal Electromechanical Properties of Low Loss (1-x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 Single Crystals,” J Appl Phys, 107 [7] 074108(2010).
177. S. Zhang, NP. Sherlock, RJ. Meyer, and TR. Shrout, “Crystallographic Dependence of Loss in Domain Engineered Relaxor-PT Single Crystals,” Appl Phys Lett, 94 [16] 162906(2009).
178. G. Liu, S. Zhang, W. Jiang, and W. Cao, “Losses in Ferroelectric Materials,” Mater Sci Eng, R, 89 1-48 (2015).
179. H. Jae Lee, S. Zhang, RJ. Meyer Jr, NP. Sherlock, and TR. Shrout, “Characterization of Piezoelectric Ceramics and 1-3 Composites for High Power Transducers,” Appl Phys Lett, 101 [3] 032902(2012).
180. K. Uchino, JH. Zheng, YH. Chen, XH. Du, J. Ryu, Y. Gao, S. Ural, S. Priya, and S. Hirose, “Loss Mechanisms and High Power Piezoelectrics,” J Mater Sci, 41 [1] 217-28 (2006).
181. K. Uchino, J. Zheng, YH. Chen, X. Du, S. Hirose, and S. Takahashi, “Loss Mechanisms in Piezoelectrics,” 25-31 Proceeding Materials Research Society Symposium, 604 (2000).
182. T. Tsurumi, “Non-linear Piezoelectric and Dielectric Behaviors in Perovskite Ferroelectrics,” J Ceram Soc Jpn, 115 [1337] 17-22 (2007).
183. T. Tsurumi, Y-B. Kil, K. Nagatoh, H. Kakemoto, S. Wada, and S. Takahashi, “Intrinsic Elastic, Dielectric, and Piezoelectric Losses in Lead Zirconate Titanate Ceramics Determined by an Immittance-Fitting Method,” J Am Ceram Soc, 85 [8] 1993-96 (2002).
184. D. Damjanovic, “Hysteresis in Piezoelectric and Ferroelectric Materials,” Sci Hysteresis, 3 337-465 (2006).
185. A. Amin, E. McLaughlin, H. Robinson, and L. Ewart, “Mechanical and Thermal Transitions in Morphotropic PZN-PT and PMN-PT Single Crystals and their Implication for Sound Projectors,” IEEE Trans Ultrason Ferroelectr Freq Control, 54 [6] 1090-95 (2007).
186. EA. McLaughlin, T. Liu, and CS. Lynch, “Relaxor Ferroelectric PMN-32%PT Crystals under Stress and Electric Field Loading: I-32 Mode Measurements,” Acta Mater, 52 [13] 3849-57 (2004).
187. HC. Robinson, “Large Signal Dielectric Losses in Electrostrictive Materials,” Proc SPIE, 3992 91-102 (2000).
188. S. Zhang, F. Li, J. Luo, R. Xia, W. Hackenberger, and T. Shrout, “Field Stability of Piezoelectric Shear Properties in PIN-PMN-PT Crystals under Large Drive Field,” IEEE Trans Ultrason Ferroelectr Freq Control, 58 [2] 274-80 (2011).
189. C. Jie, and R. Panda, “Review: Commercialization of Piezoelectric Single Crystals for Medical Imaging Applications,” pp. 235-40 In: Proceeding of IEEE Ultrasonics Symposium; 2005.
190. K. Kim, S. Zhang, W. Huang, F. Yu, and X. Jiang, “YCa4O(BO3)3 (YCOB) High Temperature Vibration Sensor,” J Appl Phys, 109 [12] 126103(2011).
191. D. Parks, S. Zhang, and B. Tittmann, “High-Temperature (> 500°C) Ultrasonic Transducers: an Experimental Comparison among Three Candidate Piezoelectric Materials,” IEEE Trans Ultrason Ferroelectr Freq Control, 60 [5] 1010-15 (2013).
193. V. Korman, GW. Hunter, JD. Wrbanek, RS. Okojie, PG. Neudeck, GC. Fralick, L. Chen, J. Xu, and GM. Beheim, “Development and Application of High-Temperature Sensors and Electronics for Propulsion Applications,” Proc SPIE, 6222 622209(2006).
194. GW. Hunter, JD. Wrbanek, RS. Okojie, PG. Neudeck, GC. Fralick, L. Chen, J. Xu, and GM. Beheim, “Development and Application of High Temperature Sensors and Electronics for Propulsion Applications,” article 622209. Proceeding of SPIE, 6222 (2006).
195. S. Zhang, Y. Fei, BH. Chai, E. Frantz, DW. Snyder, X. Jiang, and TR. Shrout, “Characterization of Piezoelectric Single Crystal YCa4O(BO3)3 for High Temperature Applications,” Appl Phys Lett, 92 [20] 202905(2008).
196. RW. Johnson, JL. Evans, P. Jacobsen, JR. Thompson, and M. Christopher, “The Changing Automotive Environment: High-Temperature Electronics,” IEEE Trans Electron Packag Manuf, 27 [3] 164-76 (2004).
197. R. Kažys, A. Voleišis, and B. Voleišienë, “High Temperature Ultrasonic Transducers: Review,” Ultragarsas, 63 [2] 7-17 (2008).
198. S. Zhang, F. Yu, R. Xia, Y. Fei, E. Frantz, X. Zhao, D. Yuan, BHT. Chai, D. Snyder, and TR. Shrout, “High Temperature ReCOB Piezocrystals: Recent Developments,” J Cryst Growth, 318 [1] 884-89 (2011).
199. S. Zhang, F. Li, W. Jiang, J. Luo, RJ. Meyer Jr, W. Cao, and TR. Shrout, “Face Shear Piezoelectric Properties of Relaxor-PbTiO3 Single Crystals,” Appl Phys Lett, 98 [18] 182903(2011).
200. X. Huo, S. Zhang, G. Liu, R. Zhang, J. Luo, R. Sahul, W. Cao, and TR. Shrout, “Complete Set of Elastic, Dielectric, and Piezoelectric Constants of [011]C Poled Rhombohedral Pb(In0.5Nb0.5)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3:Mn Single Crystals,” J Appl Phys, 113 [7] 074106(2013).
201. M. Budimir, D. Damjanovic, and N. Setter, “Piezoelectric Anisotropy-Phase Transition Relations in Perovskite Single Crystals,” J Appl Phys, 94 [10] 6753-61 (2003).
202. D. Damjanovic, M. Budimir, M. Davis, and N. Setter, “Piezoelectric Anisotropy: Enhanced Piezoelectric Response along Nonpolar Directions in Perovskite Crystals,” J Mater Sci, 41 [1] 65-76 (2006).
203. M. Davis, M. Budimir, D. Damjanovic, and N. Setter, “Rotator and Extender Ferroelectrics: Importance of the Shear Coefficient to the Piezoelectric Properties of Domain-Engineered Crystals and Ceramics,” J Appl Phys, 101 [5] 054112(2007).
204. M. Davis, D. Damjanovic, and N. Setter, “Correlation between Dielectric Anisotropy and Positive or Zero Transverse Piezoelectric Coefficients in Perovskite Ferroelectric Single Crystals,” Appl Phys Lett, 87 [10] 102904(2005).
205. DC. Lagoudas, X. Jiang, PW. Rehrig, WS. Hackenberger, and TR. Shrout, Large-Stroke Low-Profile Single-Crystal Piezoelectric Actuators, 5053 436(2003).
206. S. Dong, L. Yan, D. Viehland, X. Jiang, and WS. Hackenberger, “A Piezoelectric Single Crystal Traveling Wave Step Motor for Low-Temperature Application,” Appl Phys Lett, 92 [15] 153504(2008).
207. X. Jiang, “Single Crystal Piezoelectric Actuators for Tunable HTS Filters,” AIP Conf Proc, 823 [1] 928-35 (2006).
208. D. Stamopoulos, M. Zeibekis, and SJ. Zhang, “Modulation of the Properties of Thin Ferromagnetic Films with an Externally Applied Electric Field in Ferromagnetic/ Piezoelectric/Ferromagnetic Hybrids,” J Appl Phys, 114 [13] 134309(2013).
209. D. Stamopoulos, M. Zeibekis, and SJ. Zhang, “Control of Superconductivity by Means of Electric-Field-Induced Strain in Superconductor/Piezoelectric Hybrids,” J Appl Phys, 123 [2] 023903(2018).
210. P. Han, W. Yan, J. Tian, X. Huang, and H. Pan, “Cut Directions for the Optimization of Piezoelectric Coefficients of Lead Magnesium Niobate-Lead Titanate Ferroelectric Crystals,” Appl Phys Lett, 86 [5] 052902(2005).
211. S. Zhang, W. Jiang, RJ. Meyer, F. Li, J. Luo, and W. Cao, “Measurements of Face Shear Properties in Relaxor-PbTiO3 Single Crystals,” J Appl Phys, 110 [6] 064106(2011).
212. S. Goljahi, J. Gallagher, SJ. Zhang, J. Luo, R. Sahul, W. Hackenberger, and CS. Lynch, “A Relaxor Ferroelectric Single Crystal Cut Resulting in Large d
312 and Zero d
311 for a Shear Mode Accelerometer and Related Applications,” Smart Mater Struct, 21 [5] 055005(2012).
213. K. Kim, S. Zhang, and X. Jiang, “Surface Load Induced Electrical Impedance Shift in Relaxor-PbTiO3 Crystal Piezoelectric Resonators,” Appl Phys Lett, 100 [25] 253501(2012).
214. P. Ci, G. Liu, Z. Chen, S. Zhang, and S. Dong, “High-Order Face-Shear Modes of Relaxor-PbTiO3 Crystals for Piezoelectric Motor Applications,” Appl Phys Lett, 104 [24] 242911(2014).
215. K. Kim, S. Zhang, and X. Jiang, “Surface Acoustic Load Sensing Using a Face-Shear PIN-PMN-PT Single-Crystal Resonator,” IEEE Trans Ultrason Ferroelectr Freq Control, 59 [11] 2548-54 (2012).
216. Z-Y. Shen, Y. Tang, S. Zhang, J. Luo, Y. Li, and TR. Shrout, “Enhanced Piezoelectric Activity and Temperature Stability of [111]-Oriented Orthorhombic 0.68Pb(Mg1/3Nb2/3)O3-0.32PbTiO3 Single Crystals by Domain Size Engineering,” Scr Mater, 72-73 17-20 (2014).
217. F. Li, S. Zhang, Z. Xu, X. Wei, and TR. Shrout, “Critical Property in Relaxor-PbTiO3 Single Crystals - Shear Piezoelectric Response,” Adv Funct Mater, 21 [11] 2118-28 (2011).
218. F. Li, S. Zhang, Z. Xu, X. Wei, J. Luo, and TR. Shrout, “Temperature Independent Shear Piezoelectric Response in Relaxor-PbTiO3 Based Crystals,” Appl Phys Lett, 97 [25] 252903(2010).
219. S. Zhang, and T. Shrout, “Relaxor-PT Single Crystals: Observations and Developments,” IEEE Trans Ultrason Ferroelectr Freq Control, 57 [10] 2138-46 (2010).
220. F. Martin, HJM. ter Brake, L. Lebrun, S. Zhang, and T. Shrout, “Dielectric and Piezoelectric Activities in (1-x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 Single Crystals from 5 K to 300 K,” J Appl Phys, 111 [10] 104108(2012).
221. F. Li, S. Zhang, Z. Xu, X. Wei, J. Luo, and TR. Shrout, “Piezoelectric Activity of Relaxor-PbTiO3 based Single Crystals and Polycrystalline Ceramics at Cryogenic Temperatures: Intrinsic and Extrinsic Contributions,” Appl Phys Lett, 96 [19] 192903(2010).
222. X. Jiang, “Cryogenic Actuators and Motors Using Single Crystal Piezoelectrics,” AIP Conf Proc, 823 [1] 1783-89 (2006).
223. JB. Heaney, ML. Mulvihill, LG. Burriesci, ME. Roche, JL. Cavaco, RJ. Shawgo, ZA. Chaudhry, and MA. Ealey, “Cryogenic Deformable Mirror Technology Development,” Proc SPIE, 5172 60(2003).
224. JP. Lynch, K-W. Wang, H. Sohn, S. Sherrit, W. Zimmerman, N. Takano, and L. Avellar, “Miniature Cryogenic Valves for a Titan Lake Sampling System,” Proc SPIE, 9061 90613J(2014).
225. T-B. Xu, L. Tolliver, X. Jiang, and J. Su, “A Single Crystal Lead Magnesium Niobate-Lead Titanate Multilayer-Stacked Cryogenic Flextensional Actuator,” Appl Phys Lett, 102 [4] 042906(2013).
226. F. Yu, S. Zhang, X. Zhao, S. Guo, X. Duan, D. Yuan, and TR. Shrout, “Investigation of the Dielectric and Piezoelectric Properties of ReCa4O(BO3)3 Crystals,” J Phys D: Appl Phys, 44 [13] 135405(2011).
227. C. Shen, S. Zhang, D. Wang, T. Xu, H. Yu, W. Cao, J. Wang, and H. Zhang, “Growth and Property Characterization of CaNdGa3O7 and SrNdGa3O7 Melilite Single Crystals,” CrystEngComm, 17 [8] 1791-99 (2015).
228. F. Yu, Q. Lu, S. Zhang, H. Wang, X. Cheng, and X. Zhao, “High-Performance, High-Temperature Piezoelectric BiB3O6 Crystals,” J Mater Chem C, 3 [2] 329-38 (2015).
229. F. Chen, L. Kong, F. Yu, C. Wang, Q. Lu, S. Zhang, Y. Li, X. Duan, L. Qin, and X. Zhao, “Investigation of the Crystal Growth, Thickness and Radial Modes of α-BiB3O6 Piezoelectric Crystals,” CrystEngComm, 19 [3] 546-51 (2017).
230. M. Beaurain, P. Armand, and P. Papet, “Synthesis and Characterization of α-GaPO4 Single Crystals Grown by the Flux Method,” J Cryst Growth, 294 [2] 396-400 (2006).
231. H. Fritze, “High-Temperature Bulk Acoustic Wave Sensors,” Meas Sci Technol, 22 [1] 012002(2011).
233. HTY. Saito, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya, and M. Nakamura, “Lead-Free Piezoceramics,” Nature, 432 [7013] 84-7 (2004).
234. R. Zuo, J. Rodel, R. Chen, and L. Li, “Sintering and Electrical Properties of Lead-Free Na0.5K0.5NbO3 Piezoelectric Ceramics,” J Am Ceram Soc, 89 [6] 2010-15 (2006).
235. S-T. Zhang, AB. Kounga, E. Aulbach, W. Jo, T. Granzow, H. Ehrenberg, and Jürgen. Rödel, “Lead-Free Piezoceramics with Giant Strain in the System Bi0.5Na0.5TiO3-BaTiO3- K0.5Na0.5NbO3. II. Temperature Dependent Properties,” J Appl Phys, 103 [3] 034108(2008).
236. X. Tan, E. Aulbach, W. Jo, T. Granzow, J. Kling, M. Marsilius, H-J. Kleebe, and J. Rödel, “Effect of Uniaxial Stress on Ferroelectric Behavior of (Bi1/2Na1/2)TiO3-Based Lead-Free Piezoelectric Ceramics,” J Appl Phys, 106 [4] 044107(2009).
237. J. Rödel, W. Jo, KTP. Seifert, E-M. Anton, T. Granzow, and D. Damjanovic, “Perspective on the Development of Lead-Free Piezoceramics,” J Am Ceram Soc, 92 [6] 1153-77 (2009).
238. H. Simons, J. Daniels, W. Jo, R. Dittmer, A. Studer, M. Avdeev, J. Rödel, and M. Hoffman, “Electric-Field-Induced Strain Mechanisms in Lead-Free 94%(Bi1/2Na1/2)TiO3-6%BaTiO3
,” Appl Phys Lett, 98 [8] 082901(2011).
239. J. Rödel, KG. Webber, R. Dittmer, W. Jo, M. Kimura, and D. Damjanovic, “Transferring Lead-Free Piezoelectric Ceramics into Application,” J Eur Ceram Soc, 35 [6] 1659-81 (2015).
240. J. Koruza, AJ. Bell, T. Frömling, KG. Webber, K. Wang, and J. Rödel, “Requirements for the Transfer of Lead-Free Piezoceramics into Application,” J Materiomics, 4 [1] 13-26 (2018).
241. S. Zhang, R. Xia, and TR. Shrout, “Modified (K0.5Na0.5)NbO3 Based Lead-Free Piezoelectrics with Broad Temperature Usage Range,” Appl Phys Lett, 91 [13] 132913(2007).
242. J. Wu, D. Xiao, and J. Zhu, “Potassium-Sodium Niobate Lead-Free Piezoelectric Materials: Past, Present, and Future of Phase Boundaries,” Chem Rev, 115 [7] 2559-95 (2015).
243. K. Xu, J. Li, X. Lv, J. Wu, X. Zhang, D. Xiao, and J. Zhu, “Superior Piezoelectric Properties in Potassium-Sodium Niobate Lead-Free Ceramics,” Adv Mater, 28 [38] 8519-23 (2016).
244. X. Wang, F. Tian, C. Zhao, J. Wu, Y. Liu, B. Dkhil, M. Zhang, Z. Gao, and X. Lou, “Giant Electrocaloric Effect in Lead-Free Ba0.94Ca0.06Ti1-xSnxO3 Ceramics with Tunable Curie Temperature,” Appl Phys Lett, 107 [25] 252905(2015).
245. X. Cheng, J. Wu, X. Wang, B. Zhang, J. Zhu, D. Xiao, X. Wang, and X. Lou, “Giant d
33 in (K,Na)(Nb,Sb)O3-(Bi,Na,K,Li)ZrO3 Based Lead-Free Piezoelectrics with High T
c
,” Appl Phys Lett, 103 [5] 052906(2013).
246. M-H. Zhang, HC. Thong, YX. Lu, W. Sun, J-F. Li, and K. Wang, “(K,Na)NbO3-Based Lead-Free Piezoelectric Materials: An Encounter with Scanning Probe Microscopy,” J Korean Ceram Soc, 54 [4] 261-71 (2017).
247. W. Jo, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang, and J. Rödel, “Giant Electric-Field-Induced Strains in Lead-Free Ceramics for Actuator Applications - Status and Perspective,” J Electroceram, 29 [1] 71-93 (2012).
248. R. Wang, H. Bando, T. Katsumata, Y. Inaguma, H. Taniguchi, and M. Itoh, “Tuning the Orthorhombic-Rhombohedral Phase Transition Temperature in Sodium Potassium Niobate by Incorporating Barium Zirconate,” Phys Status Solidi RRL, 3 [5] 142-44 (2009).
249. R. Wang, R-J. Xie, K. Hanada, K. Matsusaki, H. Bando, T. Sekiya, and M. Itoh, “Phase Diagram of the (Na0.5K0.5)NbO3-ATiO3 Solid Solution,” Ferroelectrics, 336 [1] 39-46 (2011).
250. P. Li, J. Zhai, B. Shen, S. Zhang, X. Li, F. Zhu, and X. Zhang, “Ultrahigh Piezoelectric Properties in Textured (K,Na)NbO3 -Based Lead-Free Ceramics,” Adv Mater, 30 [8] 1705171(2018).
251. J. Hao, C. Ye, B. Shen, and J. Zhai, “Enhanced Electrostricitive Properties and Thermal Endurance of Textured (Bi0.5Na0.5)TiO3-BaTiO3-(K0.5Na0.5)NbO3 Ceramics,” J Appl Phys, 114 [5] 054101(2013).
252. M. Jiang, CA. Randall, H. Guo, G. Rao, R. Tu, Z. Gu, G. Cheng, X. Liu, J. Zhang, and Y. Li, “Seed-Free Solid-State Growth of Large Lead-Free Piezoelectric Single Crystals: (Na1/2K1/2)NbO3
,” J Am Ceram Soc, 98 [10] 2988-96 (2015).
253. C-H. Hong, H-P. Kim, B-Y. Choi, H-S. Han, JS. Son, CW. Ahn, and W. Jo, “Lead-Free Piezoceramics - Where to Move on?,” J Materiomics, 2 [1] 1-24 (2016).
254. CW. Ahn, HY. Lee, G. Han, S. Zhang, SY. Choi, JJ. Choi, J-W. Kim, W-H. Yoon, J-H. Choi, D-S. Park, B-D. Hahn, and J. Ryu, “Self-Growth of Centimeter-Scale Single Crystals by Normal Sintering Process in Modified Potassium Sodium Niobate Ceramics,” Sci Rep, 5 17656(2015).
255. Y-Q. Lu, and Y-X. Li, “A Review on Lead-Free Piezoelectric Ceramics Studies in China,” J Adv Dielectr, 01 [03] 269-88 (2011).
256. J. Yang, Z. Fu, Q. Yang, Y. Li, and Y. Liu, “Effect of Seeds and Sintering Additives on (K,Na,Li)NbO3 Lead-Free Single Crystals Grown by a Solid-State Crystal Growth Method,” J Ceram Soc Jpn, 124 [4] 365-69 (2016).
257. J. Yang, Q. Yang, Y. Li, and Y. Liu, “Growth Mechanism and Enhanced Electrical Properties of K0.5Na0.5NbO3 - Based Lead-Free Piezoelectric Single Crystals Grown by a Solid-State Crystal Growth Method,” J Eur Ceram Soc, 36 [3] 541-50 (2016).
258. J. Yang, F. Zhang, Q. Yang, Z. Liu, Y. Li, Y. Liu, and Q. Zhang, “Large Piezoelectric Properties in KNN-Based Lead-Free Single Crystals Grown by a Seed-Free Solid-State Crystal Growth Method,” Appl Phys Lett, 108 [18] 182904(2016).
259. H. Onozuka, Y. Kitanaka, Y. Noguchi, and M. Miyayama, “Crystal Growth and Characterization of (Bi0.5Na0.5)TiO3-BaTiO3 Single Crystals Obtained by a Top-Seeded Solution Growth Method under High-Pressure Oxygen Atmosphere,” Jpn J Appl Phys, 50 [9] 09NE7(2011).
260. S. Teranishi, M. Suzuki, Y. Noguchi, M. Miyayama, C. Moriyoshi, Y. Kuroiwa, K. Tawa, and S. Mori, “Giant Strain in Lead-Free (Bi0.5Na0.5)TiO3-Based Single Crystals,” Appl Phys Lett, 92 [18] 182905(2008).
261. M. Izumi, K. Yamamoto, M. Suzuki, Y. Noguchi, and M. Miyayama, “Large Electric-Field-Induced Strain in Bi0.5Na0.5TiO3-Bi0.5K0.5TiO3 Solid Solution Single Crystals,” Appl Phys Lett, 93 [24] 242903(2008).
262. X. Huo, R. Zhang, L. Zheng, S. Zhang, R. Wang, J. Wang, S. Sang, B. Yang, and W. Cao, “(K,Na,Li)(Nb,Ta)O3:Mn Lead-Free Single Crystal with High Piezoelectric Properties,” J Am Ceram Soc, 98 [6] 1829-35 (2015).
263. X. Huo, L. Zheng, S. Zhang, R. Zhang, G. Liu, R. Wang, B. Yang, W. Cao, and TR. Shrout, “Growth and Properties of Li, Ta Modified (K,Na)NbO3 Lead-Free Piezoelectric Single Crystals,” Phys Status Solidi Rapid Res Lett, 8 [1] 86-90 (2014).
264. D. Lin, S. Zhang, C. Cai, and W. Liu, “Domain Size Engineering in 0.5%MnO2-(K0.5Na0.5)NbO3 Lead Free Piezoelectric Crystals,” J Appl Phys, 117 [7] 074103(2015).
265. J. Yao, N. Monsegue, M. Murayama, W. Leng, WT. Reynolds, Q. Zhang, H. Luo, J. Li, W. Ge, and D. Viehland, “Role of Coexisting Tetragonal Regions in the Rhombohedral Phase of Na0.5Bi0.5TiO3-xat.%BaTiO3 Crystals on Enhanced Piezoelectric Properties on Approaching the Morphotropic Phase Boundary,” Appl Phys Lett, 100 [1] 012901(2012).
266. C. Chen, X. Jiang, Y. Li, F. Wang, Q. Zhang, and H. Luo, “Growth and Electrical Properties of Na1/2Bi1/2TiO3-BaTiO3 Lead-Free Single Crystal with Morphotropic Phase Boundary Composition,” J Appl Phys, 108 [12] 124106(2010).
267. Q. Zhang, X. Li, R. Sun, X. Wu, B. Ren, X. Zhao, and H. Luo, “Electric Properties of Mn Doped 0.95Na0.5Bi0.5TiO3-0.05BaTiO3 Crystal after Different Annealing Processes,” J Cryst Growth, 318 [1] 870-73 (2011).
268. J. Yao, Y. Yang, N. Monsegue, Y. Li, J. Li, Q. Zhang, W. Ge, H. Luo, and D. Viehland, “Effect of Mn Substituents on the Domain and Local Structures of Na1/2Bi1/2TiO3-BaTiO3 Single Crystals near a Morphotropic Phase Boundary,” Appl Phys Lett, 98 [13] 132903(2011).
269. X. Li, C. Chen, H. Deng, H. Zhang, D. Lin, X. Zhao, and H. Luo, “The Growth and Properties of Lead-Free Ferroelectric Single Crystals,” Crystals, 5 [2] 172-92 (2015).
270. M. Ogino, Y. Noguchi, Y. Kitanaka, M. Miyayama, C. Moriyoshi, and Y. Kuroiwa, “Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3-BaTiO3 Single Crystals under Electric Fields,” Crystals, 4 [3] 273-95 (2014).
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||