Full Parametric Impedance Analysis of Photoelectrochemical Cells: Case of a TiO2 Photoanode
Article information
Abstract
Issues in the electrical characterization of semiconducting photoanodes in a photoelectrochemical (PEC) cell, such as the cell geometry dependence, scan rate dependence in DC measurements, and the frequency dependence in AC measurements, are addressed, using the example of a TiO2 photoanode. Contrary to conventional constant phase element (CPE) modeling, the capacitive behavior associated with Mott-Schottky (MS) response was successfully modeled by a Havriliak-Negami (HN) capacitance function-which allowed the determination of frequency-independent Schottky capacitance parameters to be explained by a trapping mechanism. Additional polarization can be successfully described by the parallel connection of a Bisquert transmission line (TL) model for the diffusion-recombination process in the nanostructured TiO2 electrode. Instead of shunt CPEs generally employed for the non-ideal TL feature, TL models with ideal shunt capacitors can describe the experimental data in the presence of an infinite-length Warburg element as internal interfacial impedance – a characteristic suggested to be a generic feature of many electrochemical cells. Fully parametrized impedance spectra finally allow in-depth physicochemical interpretations.
1. Introduction
Photoelectrochemical (PEC) cells have been investigated intensively in recent years for their use as light-to-electrical energy conversion devices. Recently, Si-doped TiO2 nanorods-prepared by the hydrothermal method-have been investigated as photoanodes for water splitting. Nominally 2% Si-doped TiO2 nanorods were shown to exhibit higher performance when compared with the pristine TiO2.1) In this work, a similarly prepared 5% Si-doped TiO2 sample was examined in a different experimental setup. Electrical characterizations using nonstandardized, three-electrode, photoelectrochemical setups are plagued with artefacts depending on the chamber geometry, position of electrodes, illumination conditions, etc., and thus are poorly reproducible and often incompatible.2) Using this work as an example, several general issues regarding the electrical characterization of PEC cells are addressed.
Typical electrical characterizations of PEC cells include DC and AC analyses: 1) (Direct) current-voltage (or potential) (I-V) characteristics measured often with a chopped white light source for PEC performance over a potential range of interest. 2) Incident-photon-to-current-conversion-efficiency (IPCE) where photo- and dark current are similarly measured at a fixed electrochemical potential over the spectral range of interest. The efficiency is estimated with respect to the response of the reference silicon photodiode. 3) Capacitance-voltage (C-V) characteristics for Mott-Schottky (MS) analysis conventionally measured at chosen fixed frequencies of AC oscillations, usually in dark conditions, similarly as for the semiconductor junctions in solid state electronic devices.3) As the semiconductor/liquid electrolyte junctions are easily made, MS analysis may be conveniently applied to a PEC configuration for semiconductor characterizations.
TiO2 electrodes are also the photoelectrodes of dye-sensitized solar cells (DSSCs). TiO2 electrodes in contact with organic electrolytes for DSSCs may suggest some similarity with those in PEC cells. In-depth parametric impedance spectroscopy for DSSCs with nanostructured TiO2 electrodes, developed over more than a decade,4–10) features transmission line (TL) models for the electron diffusion-recombination process. The diffusion-recombination mechanism is suggested as being applicable for TiO2 electrodes of DSSCs which are i) low-doped, i.e. of small carrier concentration, and ii), nanostructured, so that the electron charge in the nanostructured TiO2 is compensated by the positive ion charge of the surrounding organic electrolyte and thus no electrical potential gradient or electron drift occurs.
TL model responses are also indicated in nanostructured TiO2 in aqueous cells, as for PEC water splitting,9) so the applicability of the TL impedance model may be considered for PEC electrodes, as in this work. As introduced above, MS analysis is a typical AC characterization of PEC cells, but usually one fixed frequency response is monitored as a function of potentials. MS analysis assumes highly doped semiconductors, where the charge depletion or accumulation is limited at the interface, regardless of the feature size. It should be noted however, that the doping concentration of the semiconductor electrodes for DSSCs or PEC cells, including this work, is seldom controlled or well-defined. Often developed in diverse meso- and nanoporous structures aiming at high performance,11–13) photoanodes are likely to have strong microscopic inhomogeneity in the doping concentration, in surface potentials, and also in the feature size. Therefore, the diffusion-recombination mechanism in the response of a PEC electrode may not be a priori excluded. The porous nanostructured PEC electrodes may be low-doped, so that the applied potential changes the Fermi level homogeneously in the electrode layer.4–10)
In fact, the two different impedance mechanisms or models concern different relevant potential (bias) ranges: 1) MS behavior applies to the depletion of majority charge carriers in TiO2 electrodes under reverse bias; 2) The diffusion-recombination mechanism in DSSCs is most prominent under forward bias near open circuit voltage (OCV), where the charge carrier concentration in TiO2 electrodes increases. The two mechanisms are considered together in semiconductor devices containing pn junctions where the majority charge carrier depletion at the interface and minority charge carrier diffusion and storage occur.14,15) Two capacitance terms, depletion and diffusion, are added together. The electrical behavior of organic bulk heterojunction solar cells is also described by combination of the depletion capacitance and diffusion.16) It should be mentioned that TL model response can also be ascribed to the distributed resistor and capacitor components of porous metallic electrodes17) or the percolating network in the insulating matrix,18) not related to the diffusion-related processes.
In this work, therefore, the co-presence of the two mechanisms is suggested in the AC response of a TiO2 photoanode. Importantly, it is shown how non-trivial huddles in the parametric description of two mechanisms are successfully overcome. The prospect is considered bright for the systematic examination and comprehensive understanding of the semiconducting oxides for water splitting.
2. Experimental Procedures
The PEC properties of 5% Si-doped, TiO2 nanorods were examined in a lab-made PEC test station reported earlier.13) The experimental setup included a miniature PEC cell, a xenon lamp (LS-150, ABET Technologies Inc., USA), a custom-made automatic chopper, a monochromator (Spectro, Korea), and a potentio/galvanostat with a frequency response analyzer (Autolab PGSTAT 302N FRA2, The Netherlands), as shown in Fig. 1(a). A close-to-scale schematic diagram of the setup is shown as S1 in Fig. 1(b). The miniature quartz cell was designed by drilling a hole in a commercial optical cuvette (12.5 × 12.5 × 45 mm3) where the semiconductor electrode was fixed using a rubber O-ring from outside. The 3 mm diameter hole size defines the electrode area in contact with the electrolyte as 7 mm2. A commercial Ag/AgCl reference electrode (RE-ICP, ALS Co., Japan) and a Pt mesh counter electrode were used for a three-electrode configuration. Aqueous solution 0.1 M NaOH (pH=13) was used as an electrolyte. I-V characteristics were measured during the light-off and light-on cycles with the chopping period of 10 s. Different scan rates were tested at 0.02 V·s−1 and 0.005 V·s−1. Electrochemical impedance spectroscopy (EIS) was performed as a function of the anodic potential at 0.1 V intervals with AC peak amplitude of 10 mV. The IPCE measurement was carried out for the wavelength range of 300 nm to 600 nm, at a scan rate 1 nm·s−1. Light intensity was calibrated using a silicon reference cell (BS-500 S/N 017, Bunkoukeiki Co., Ltd, Japan).
3. Results and Discussion
3.1. I-V characteristics and IPCE
Figure 2(a) shows I-V curves with scan rates 0.02 V·s−1, except one at 0.005 V·s−1 which is presented alone in Fig. 2(b) and (c), at the same light chopping period of 10 s. Several measurements using setups S1 and S2, as shown in Fig. 1(b), were performed for the same sample. Although the results are not completely reproducible, a systematic difference between the two reference electrodes was confirmed. The increase in cathodic currents was higher with the commercial reference electrode R1, than R2, a lab-made one, which is nominally of the same structure, i.e. Ag/AgCl in saturated KCl. When tested together in different electrolytes, there was negligible difference in the OCVs between the two reference electrodes. The origin of the difference between the two reference electrodes under cathodic condition is not clear yet. It should be noted that the measurements with R2 suggest larger onset potentials (more negative) than those with R1. In fact, as shown in the inset of Fig. 2(a), all the measurements exhibit OCV at around −0.2 V vs. Ag/AgCl in dark conditions, regardless of the setup and reference electrodes. The coincidence of the light-insensitive cathodic curves for the comparative measurements in different setups S1 and S2 suggests that the electrode area is well-defined by the hole sizes as 3 mm and 5 mm, respectively, for S1 and S2. Other differences between the two setups should be ascribed to the quartz cell size and the position and geometry of the counter electrodes, with respect to the photoanodes, as shown in Fig. 1(b). The electrolyte volume and path length in S2 are much larger than in S1. An increase in dark anodic current above 1 V is also notable, which may be described as breakdown or leakage. Very low breakdown voltage is not uncommon in nanostructured or thin film diodes for solar cells or LEDs, and can be attributed to leakage. For the thick, single, crystalline TiO2 sample reported by Honda and Fujishima,19) and ZnO single crystalline photoanodes with diffusion-bonded Pt back contact,20) very stable reverse behavior up to a few volts were observed. On the other hand, very leaky I-V behavior was observed for the ZnO films prepared by the solution method, which was moderated by the formation of a denser seed layer.13) The larger leakage current density for the larger electrode area of S2 appear to support the nature of the breakdown spots, in contrast to the behavior of cathodic currents proportional to the electrode area. The difference in the anodic photocurrents between setups shows unequal illumination conditions. The very small electrolyte volume in the S1 setup appears to cause greater irreproducibility in the dynamic measurements.
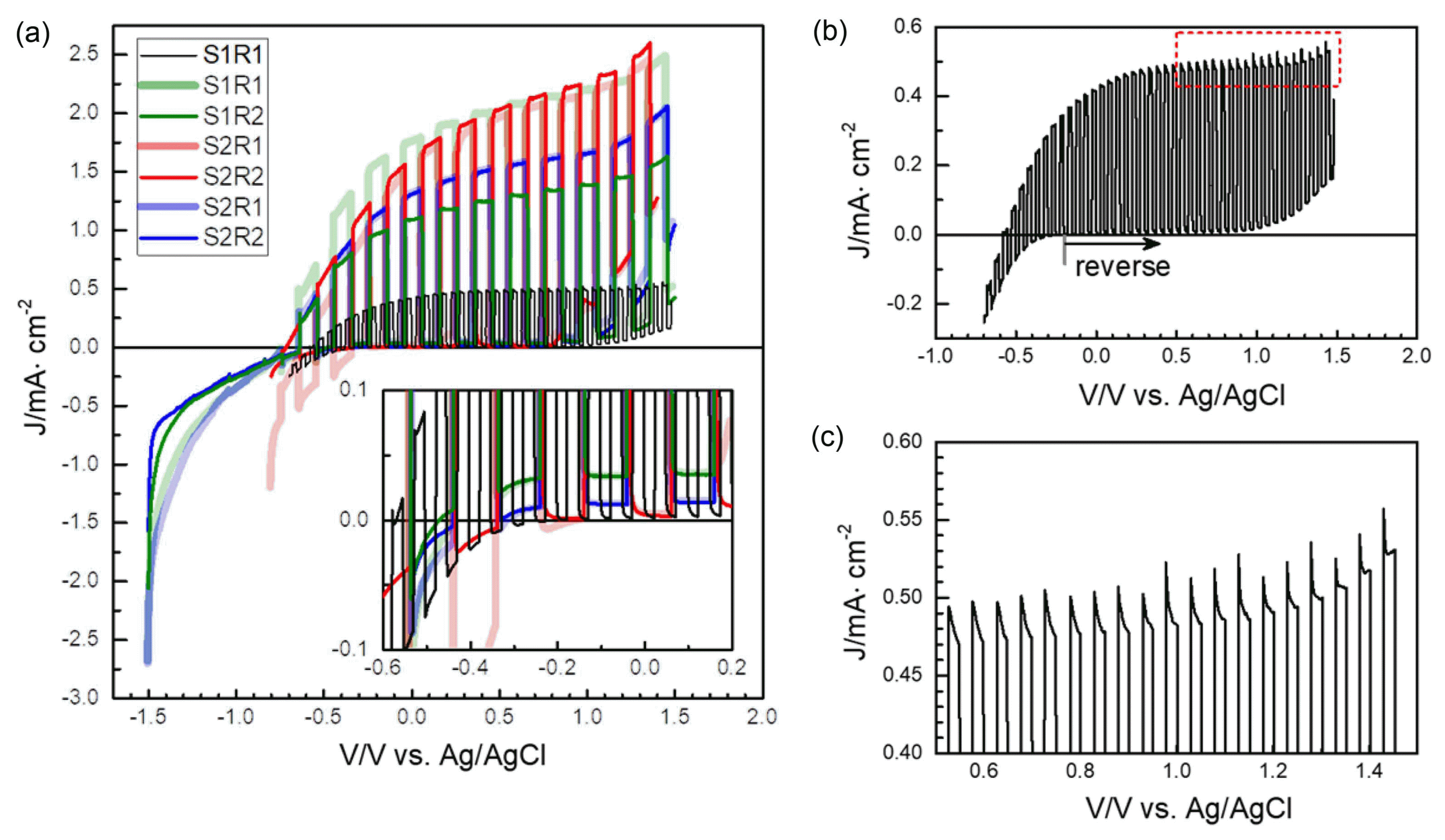
(a) I-V characteristics with light on/off for 10 s periods using different setups and different reference electrodes, as indicated in Fig. 1(b). Inset shows the magnification near OCV in the dark. The scan rates are 0.02 V·s−1 except as presented in (b) and (c). (b) I-V curve in S1 using R1 at the scan rate of 0.005 V·s−1. (c) The enlarged image of the boxed region of Fig. 2(b).
I-V characteristics also depend on the scan rates and the light chopping speed or periods. Slower scan rates generally reduce the photocurrents, as well as dark currents, as shown by the data scanned at 0.005 V·s−1 in Fig. 2(b). The spikes of the photocurrents for the boxed region are shown more clearly in Fig. 2(c). They were attributed to the accumulated photoexcited holes at the semiconductor-electrolyte interface.21,22) The spiky behavior is pronounced at the high reverse bias above 0.7 V (vs. Ag/AgCl). With the constant voltage scan rate of 0.005 V·s−1, the relaxations are shown to be faster at high reverse bias, which seems contradictory to the discussion attributing them to the accumulated photoexcited holes at the semiconductor-electrolytes interface. The increasing contribution of the fast relaxation may be related to the increasing high frequency ohmic contribution, ROHM, distinguished by the impedance spectroscopy presented in the next section. Strong scan rate dependence can be ascribed to slow relaxation of the electrochemical response in PEC cells, corresponding to the low frequency impedance behavior. There is also often temporal change involved, since non-zero DC currents cause the evolution in mass and charge concentration in bulk, and at interfaces, and the irreversible or very slowly recovering drift in the cell responses occurs. The situation is in contrast to photovoltaic solar cells associated with much faster electronic relaxations only.
Figure 3 presents IPCE spectra measured at different potentials. The IPCE exhibits the onset wavelength at approximate 454 nm, enabling an energetic bandgap of 2.74 eV to be calculated. The maximum IPCE of the sample is about 26%. The IPCE is shown slightly higher at 0.5 V than at 0.3 V, and both are distinctly higher than that at 0 V. It should be noted that the potential dependence simply reflects the photocurrents in Fig. 2, since IPCE is nothing other than the net photocurrents normalized with respect to the response of the silicon standard cell with the calibrated light intensities. In this work, almost continuous scans at 1 nm·s−1 and at 1 nm steps were made, so that the spectra provided the detailed wavelength dependence. The continuously measured spectra were found to be comparable in their peak shapes and magnitudes with previously reported1) stepwise measurements. In steady-state measurements, values are taken at each wavelength after some relaxation time, e.g., at 20 nm intervals.1) The photocurrents under monochromated illumination for IPCE exhibit relaxations or time-dependence, similarly as those under full sun condition discussed above. Steady-state currents should be taken at each potential after some transient behaviors. The waiting time is often fixed, e.g. 5 s, for the systematic automated measurement. IPCE measurements of PEC cells therefore have the same inherent issues discussed above for the I-V characteristics. IPCE spectra measured continuously, as in Fig. 3, may be recommended over the broken spectra from step-wise measurements. With the experimental scan rates given and taken into consideration, the detailed wavelength dependence, such as peaks and shoulders, provides rich information on the electronic structure of photoanodes.
3.2. Mott-Schottky Analysis and Issues
Mott-Schottky (MS) analysis is based on the response of the Schottky space charge depletion region of the semiconducting photoanode, which behaves as a capacitor with the thickness of the depletion layer at the interface with the electrolyte controllable by external potentials. The capacitance-voltage (C-V ) characteristics obtained by a frequency response analyzer (FRA) combined in a potentio/galvanostat, well-known for the similarly generated depletion layer at semiconductor/metal contact, follow the relationship shown in Eq. (1):
The analysis provides the donor concentration ND of the semiconducting anode from the slope, and the flatband potential VFB from the intercept. Although MS analysis is routinely performed for the characterization of PEC cells, there are problematic issues. In contrast to the flat semiconductor/metal Schottky junction, porous nanostructured photoanodes in PEC cells do not provide well-defined area A in Eq. (1). The high performance of the nanostructured electrodes, e.g. photocurrent density J in Fig. 2, is often firstly ascribed to the enlarged effective area, much larger than the macroscopic electrode area evaluated e.g. from the holes with diameter 3 mm or 5 mm in Fig. 1(b). The area A is directly involved in the estimation of ND for the given capacitance response, thus ND estimates can be several orders different, depending on the estimation of A. The exact evaluation of the interface area is generally difficult. The situation is illustrated for the present system in Fig. 4. For the typical TiO2 nanorods of 0.5 × 0.5 × 2.5 μm,1) the top surface area of 0.25 μm2 is only 5% of the lateral side area of 5μm2.
For a TiO2 system, the dielectric constant ɛR in Eq. (1) also needs some consideration. For most covalent or ionic semiconductors, the static dielectric constants ɛR around 10 are contributed by the atomic (electronic) and ionic contribution, which are independent of frequencies in the range concerned here, and also of temperature. TiO2 in this work, however, similarly as SrTiO3 and KTaO3, is classified as incipient ferroelectric material, based on the experimental observation that its dielectric permittivity ɛR is exceptionally large, and increases with decreasing temperature.23) At 300 K, ɛR values along the c-direction and a-direction of the tetragonal rutile structure are 170 and 86 respectively. On the other hand, strong pseudo-dielectric effects due to electronic and ionic conduction mechanisms are also observed in the TiO2 system, which increases with increasing temperature.24) As emphasized recently for ionic conductors,25–28) these apparent dielectric effects from mobile charge carriers should be distinguished from the true dipolar polarization considered for the dielectric constant ɛR in Eq. (1). Therefore, it may not always be clear which dielectric constants should be used or how to consider possible anisotropic effects. Although the evaluation of VFB is not formally affected by A or ɛR in Eq. (1)VFB can also vary microscopically due to the different surface structure and chemistry of porous electrodes.
There are also thickness effects. For thin film electrodes, saturation of the depletion capacitance occurs under high reverse bias. Similarly, as illustrated in Fig. 4(c), the effective surface area of the nanostructured electrodes decreases with increasing depletion thickness, upon high reverse bias. This was suggested to explain the upwardly curved MS plot of nanostructured Fe2O3 electrodes,29) and the roughness at the top surface of TiO2 nanorods,1) as schematically shown in Fig. 4(b), may give rise to similar outcomes.
All these issues, related to poorly defined geometry factors of the nanostructured photoanodes, are very specific and difficult to be address precisely. Microstructural features that are complicatedly heterogeneous may explain the co-presence of the space charge depletion effects for the highly doped semiconductors and the diffusion-recombination kinetics described by the TL model and expected for the low-doped nanostructured electrodes, are discussed in later sections (Sec. 3.4 & 3.5).
3.3. Capacitance Spectra and the Havriliak-Negami Equation
A more general critical issue in MS analysis is the so-called frequency dispersion, or the frequency dependence, of the measured capacitance. The real capacitance values are directly given by the relationship with impedance data as C* = (jωZ*)−1 = C′ – jC″ for a measured frequency f = ω/2π. If the system behaves as an ideal capacitor of capacitance C with impedance (jωC)−1, the same capacitance results, regardless of the measured frequency values chosen. However, frequency-dependent capacitances and nonlinear MS relationships have been observed even in well-defined single crystalline electrodes,30,31) let alone in various nanostructured electrodes. Therefore, the capacitance component evaluated at an arbitrary frequency, e.g. 1 kHz, could not properly represent the Schottky capacitance CSB in Eq. (1) for the depletion layer at the semiconductor/electrolyte interface.
Parametrized capacitance obtained by impedance model analysis could address the frequency dispersion issue. A few parametric impedance spectroscopy results for CSB components have been reported.29,32,33) There is a common criticism, however, that equivalent circuit parameters are strongly model-dependent. Currently, in many different subjects and systems, including PEC cells, the impedance model analysis employs so-called CPEs (constant-phase-elements) of the complex capacitance
Since the Schottky junction is largely capacitive and highly resistive (see Fig. 9 below), the impedance plane presentation of the AC response of PEC cells under anodic condition is not very informative. The capacitance information is better shown by the complex capacitance plane graphs presented in Fig. 5. In this work, the impedance is measured from 1 MHz to 0.1 Hz in logarithmic sweeps at the voltage interval of 0.1 V. While the resistor-capacitor parallel connection, or (RC), leads to the semicircular arc in the impedance plane, the capacitance arcs distinguished in all the spectra may be roughly described by the resistor-capacitor series circuit or ‘Debye’ circuit which is overlapped by the lower frequency response. (The resistor component is the high frequency ohmic response best distinguished in the high frequency region of the impedance spectra, as indicated in Figs. 9(d) and (h)). Systematic variation according to the MS relation is best shown in Fig. 5(b), for the potential range between 0.0 V and 0.6 V, where the capacitance decreases with increasing reverse bias. It is also notable that the local minima near 10 Hz (or Log (10/Hz) = 1), bounding the high frequency capacitance arc from the lower frequency response, lie on one line represented by the dashed line. Systematic variation can be found at different frequencies, e.g. at 100 Hz (or Log (100/Hz) = 2). MS plots for the frequencies 10, 100, and 251 Hz are shown in Fig. 8(c). MS linear relationships may be found for the plots at 10 and 100 Hz, but with different slopes and intercepts thus resulting in different ND and VFB values. The frequency of 1 kHz, used in the previous work,1) gives little indication of an MS relationship. (Note that the data lies out of the range and thus is not shown.)

Selected spectra in impedance planes. Except for (h), the spectra match those of Fig. 7. The finite magnitude of Bisquert TL element RBQ is indicated in (c), (d), (e), and (h) for the forward and leaky reverse biases. The dashed blue lines are the Bisquert response without interfacial Warburg impedance, QW. The red dash-dotted lines represent the response without Schottky capacitance in parallel, represented by the HN equation. For the spectrum in (d), chemical or shunt capacitance CP, dominated by QW, was not evaluated. For the spectrum (h), Schottky capacitance was not deconvoluted.

Complex capacitance spectra in dark (a, b, c) and illuminated ‘light’ conditions (d, e, f); Near flat band voltage (a, d); reverse bias (b, e) and high reverse bias or leakage region (c, f). The numbers on the close symbols represent the logarithmic frequency values. The lines are simulated spectra using the fit results shown in Fig. 6.

Mott-Schottky plots of Schottky capacitance CSB under dark (a) and illuminated (b) conditions. In (a) Mott-Schottky analysis is from the data range between 0.2 V and 0.6 V vs. Ag/AgCl. In (c), capacitance values at the frequencies 10 Hz, 100 Hz, and 251 Hz are compared with CSB. The results from Ref. 1 are also presented.
The solution to all these troubles is the parametric impedance spectroscopy. When the response is explained by the plausible model, including the capacitance parameter CSB, a frequency-independent, and uniquely defined CSB can be obtained for each spectrum, or for each potential. It should be noted that CPE was first introduced by Cole and Cole for the non-ideal Debye behavior of the dielectric system,35) with reference to the ideal RC series circuit, where the capacitance effects are represented by the ideal capacitor and the dispersion is represented by a CPE with α close to 0 limit corresponding to an ideal resistor. Later, the Havriliak-Negami (HN) equation is suggested as a more general description of the dispersive dielectric responses:36)
With γ = β = 1, the equation represents the Debye response, where τ = RC. Note that the Debye circuit is also the model for the relaxation process involving deep trap levels in Schottky diodes.37) The HN equation can thus represent the dispersive, distributed, or non-ideal trapping processes associated with the Schottky junction. Unlike CPE, the equation provides well-defined limiting capacitance magnitude CHN, which can be interpreted for physical interpretation as in Eq. (1). Recently, capacitance effects represented by HN functions connected in parallel have been shown to give more superior descriptions of the impedance behavior of many polycrystalline solid electrolytes.25–28) Eq. (2) is implemented as model DE-31 in a ZView program (Scribner Ass. Inc., USA), as indicated in the equivalent circuit model shown in Fig. 6, center left. In previous publications,26,28) ‘H’ symbol was introduced for a simple equivalent circuit diagram. (Note that the model number in the program has been changed from “DE-28 reported earlier.28)) This is a versatile model, and is expected to play a crucial and essential role in the future impedance spectroscopy.
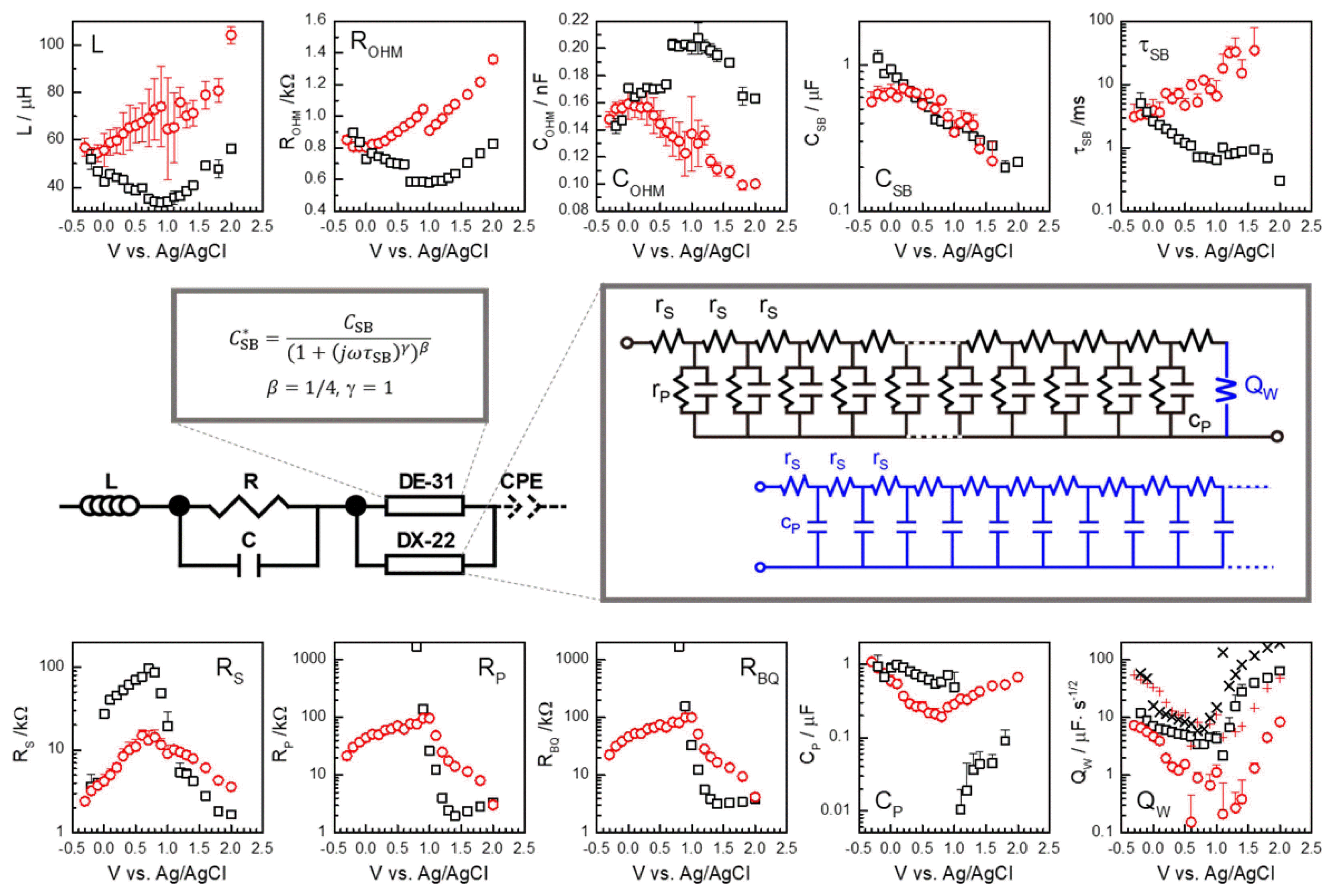
General impedance model for photoanodes of PEC cells (middle) and the parameters in dark (black squares) and illuminated conditions (red circles) at different potentials. Note that only the upper plus side of the errors is shown, for clarity in the logarithmic plots (RS, RP, RBQ, CSB, τSB, CP, QW). See the text for details.
According to the full parametric analysis, including the Bisquert TL model (DX-22§, in Fig. 6) for the diffusion-recombination process as described in the following section, at least for the reverse bias exhibiting the systematic variation as in Fig. 5(b), the power exponents were found almost constant close to β = 1/4 with γ = 1, that is:
The final fitting presented here was performed with fixed exponents for all spectra. Small variations in the fitted exponents led to strongly correlated variations in the other fitted parameters, so the exponents to be fixed should be determined by preliminary fitting procedures, or by theory if any.25–28)
It should be noted that the apparent capacitance arcs in the experimental spectra of Fig. 5 are largely ascribed to the series ROHM components, as shown by the simulation represented by dashed blue lines in Fig. 7. Separately simulated HN components of Eq. (3) are presented in dash-dotted red lines. At the high frequency range ω→∞, the equation behaves as CPE or Q with α = 3/4, with the constant angle of (1–α) (π/2) or π/8. The dispersion in the Schottky capacitance can be attributed to the distribution of donor or trap levels in the TiO2 photoanode, with reference to the case of γ = β = 1 for the single trap level. Whether the exponent β = 1/4 should have any mechanistic origin needs further investigation in related and other semiconducting photoanodes or Schottky junctions.
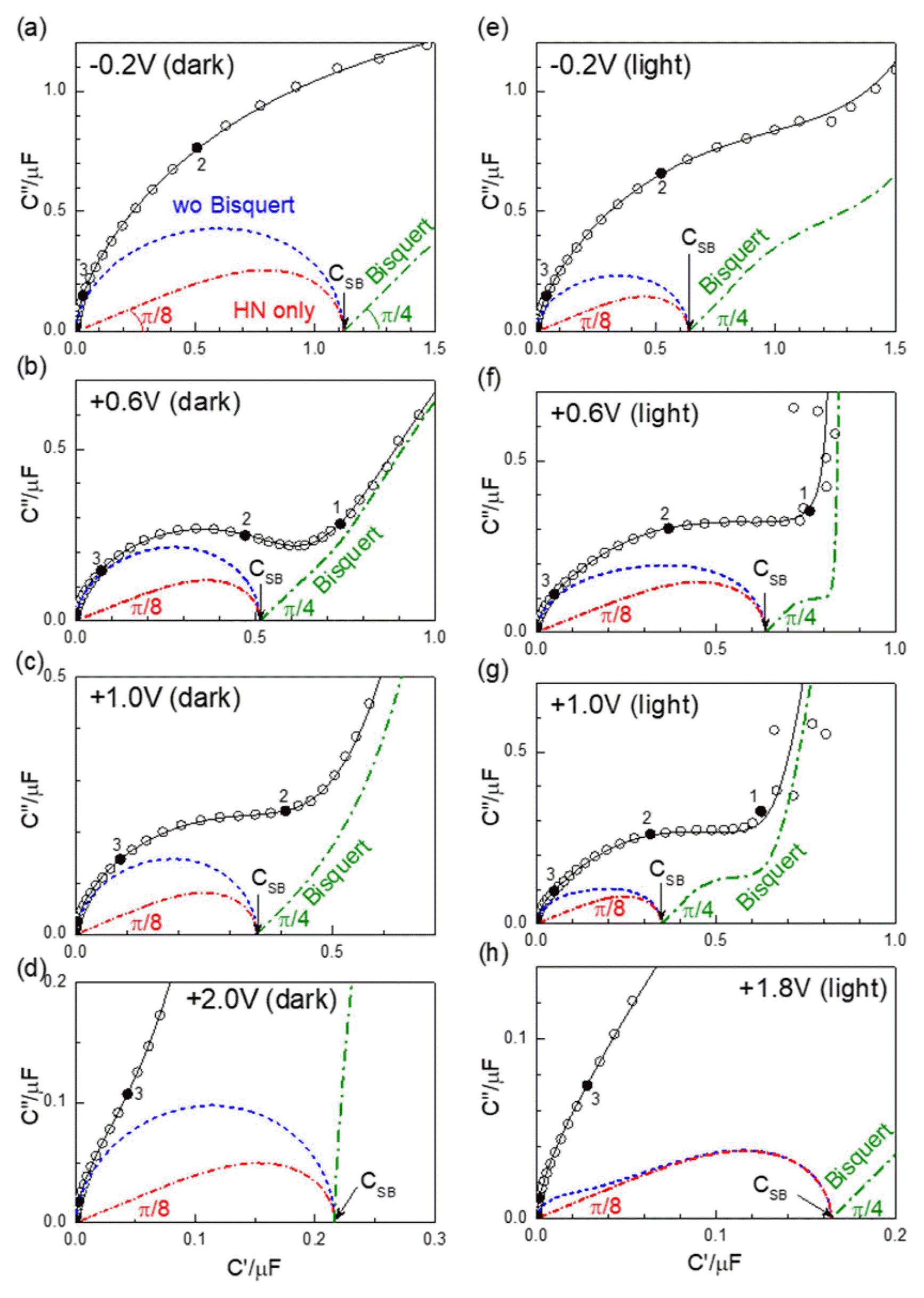
Selected examples of the capacitance spectra in dark condition ((a)–(d)) and under illumination ((e)–(h)) at different potentials vs. Ag/AgCl. Simulated HN elements for distributed Schottky capacitance are shown in red dash-dotted lines, with high frequency responses of the phase π/8. The dashed blue lines represent the simulation, including the high frequency response described by L and RC parallel circuits, but without the Bisquert TL element (DX-22) (Fig. 6). The Bisquert model in parallel to CSB is shown in green dash-dotted lines. The high frequency response of the constant phase π/4 is indicated for the spectrum with finite CP.
Identification of such components with well-defined power exponents was made possible, since the frequency dispersion parameters for the overlapping Bisquert components, discussed in the next section, are used in the ideal form given by the theoretical model. If multiple frequency dispersion parameters such as α in CPE or γ and β in HN function were left free, there would be little chance to systematically determine model parameters of any physical significance. Frequency power exponents affect the impedance response over the wide frequency range, so it is highly likely that all other fitted parameters would end up strongly correlated with these exponents, just to reach the minimum of the sum of squared errors in the fitting process. This discussion points out the critical problem in the impedance spectroscopy in many different subjects and studies, where modeling with multiple ‘magic’ CPEs, as (R1Q1)(R2Q2)(R3Q3), allows a very nice description of the experimental spectra, but further significance is barely considered.
The fitted CSB and τSB parameters of Eq. (3) are presented in Fig. 6, together with other parameters. The somewhat abrupt change in CSB and τSB between 0.6 V and 0.7 V in dark condition is in accordance with the behavior of the raw experimental data. The feature is most clearly indicated in the parameters for the high frequency responses L, ROHM, and COHM in Fig. 6. Unlike the continuous voltage scanning of potential for the current or for the monofrequency impedance conventionally done, wide frequency range impedance measurements with stepwise change in the potential, as done in this work, cause some difficulty in obtaining systematically varying reproducible raw data sets. Faradaic currents affect cell behavior during measurements, both temporarily and in the longer term.
Figure 8(a) presents MS plots of parametrically obtained CSB. A well-defined linear relation can be found between 0.2 V and 0.6 V. According to Eq. (1), using the macroscopic electrode area defined by the hole in the quartz cuvette, 7 mm2, ND and VFB were estimated as 3.2 × 1019 cm−3 and 0.17 V vs. Ag/AgCl, respectively. It is notable that a similar MS slope was indicated above 0.7 V. Consistent ND values may be estimated with some difference in the intercept or VFB as 0.35 V. The shift in the intercept, or VFB, may be explained by the change in surface polarization state, or the formation of the Helmholtz layer at the solution side of the interface during the measurements. The deviation below 0.2 V is ascribed to the potential approaching VFB and cathodic range.
In the measurement under illumination, a discontinuity occurred between 0.9 V and 1.0 V. This is shown in the parameters L, ROHM, and COHM, and less clearly in CSB and τSB, all represented by red symbols in Fig. 6. The corresponding MS plot is given in Fig. 8(b). The parameters evaluated from the data under illumination are shown associated with large errors, except ROHM. Note that large statistical errors are generally associated with overparameterization. The broad capacitance response of Fig. 7(e), (f), and (g) under illumination is described by the overlapping responses of an HN function (DE-31), and a Bisquert TL model (DX-22), as well as of other components for the high frequency response. This is in contrast to the measurement in dark conditions, where the magnitude of CSB is rather directly indicated in the raw capacitance spectra. Moreover, the low frequency measurements under illumination conditions were very poor. Under such limitations, an MS behavior is suggested at high reverse bias above 0.5 V. Using a slope similar to that for dark conditions, VFB may be extrapolated near 0 V. The difference from the dark condition may be qualitatively explained by the decrease in Schottky barrier potential, consequent to the photoinduced charge carriers.
In Fig. 8(c), parametric CSB from Fig. 8(a) and some monofrequency MS plots are compared. The results are in great contrast to the MS plots at 1 kHz reported earlier1) using the S2 setup in Fig. 1(b) for the pristine and 2% Si-doped TiO2 nanorods. The AC behavior is completely different from the present work using the S1 setup, and the substantial differences between the two measurements can be mainly attributed to the setups. Different quartz vessels and different positions of the electrodes, as shown by S1 and S2 in Fig. 1(b), result in different high frequency responses, which is strongly affected by the ohmic contribution. Moreover, the near VFB and cathodic potential are strongly affected by the reference electrodes, R1 and R2, as illustrated in Fig. 2(a). The difference in VFB or OCV is also partly explained by the pH value, 14, used in the previous work compared with this work (pH 13), which increases VFB by 0.059 V at RT. Fresh TiO2 electrodes exhibit higher VFB. Repeated measurements of the samples as in this work, may have changed ND, for example by proton uptake by electrochemical doping,9) or the surface chemistry, for example by the redistribution of Si or any other built-in surface charges even with thorough washing in between.
For the data shown in Fig. 8(c) from the previous report,1) the MS analysis was made for the frequency range around −0.5 V vs. Ag/AgCl, indicated in solid lines, which resulted in the conclusion of the same VFB of 0.75 V vs. Ag/AgCl for both samples, i.e. same intercepts and larger ND for Si-doping from the lower slope. The result was supposed to represent the increased electron concentration by Si doping. However, when the linear behavior around −0.2 V is considered, similar slopes mean essentially the same ND for both samples, hence, no bulk doping effects. VFB of 1.0 V for the pristine sample, and 0.85 V for the Si-doped sample, may be attributed to the Si segregation on the surface. In fact, Si has negligible solubility in TiO2. The effects on the chemical diffusivity and electrical conductivity in TiO2 containing SiO2 as composites were attributed to the alteration in concentrations of transport-related point defects by the transfer of charged species to internal surfaces.38)
The discussion above illustrates the issues associated with the MS analysis, which are the frequency dependence (or dispersion) and potential range dependence, and the consequent controversies in scientific interpretations. The problem with having poorly defined geometry in porous nanocrystalline photoanodes was discussed above using Fig. 4. The ND estimated as 3.2 × 1019 cm−3 according to Eq. (1), using the hole area of 7 mm2 and ɛR 170 for c-direction, show that TiO2 is highly doped. The CSB of approximately 0.7 μF at 0 V vs. Ag/AgCl corresponds to a 15 nm thickness of the depletion space charge layer. However, if the true surface area of the electrode with TiO2 nanorods becomes 100 times larger, it would reduce the estimation of ND by 104 times, i.e. 3.2 × 1015 cm−3, which is very low-doping. The depletion layer thickness becomes 1.5 μm and all nanorods would be electron depleted. When the lateral surface of the c-axis-oriented TiO2 rods is considered, ɛR in the perpendicular direction 86 should be used, which increases ND twice and decreases the thickness of the depletion layer by half.
The strong variation of the ohmic resistance ROHM for this measurement set, with potential and also with the illumination, is peculiar. In other measurements, the potential-independent ohmic resistance of the electrolyte of about 400 Ω was observed. The additional resistance may be attributed to the effective resistance of the film of TiO2 nanorods, which changes with the potential and illumination condition. Increasing resistance with reverse bias suggests the effects of the depleted electron charge carriers over a significant portion of the sample or nanorods. Fig. 6 illustrates that the L and COHM parameter explain the high frequency behavior in a manner correlated with that of ROHM.
3.4. Bisquert TL Model with ZB
For a purely semiconducting Schottky diode, the impedance should end up being purely capacitive, as shown by the simulated HN response in Fig. 7, and possibly with leakage current, represented by a parallel resistor RDC, which gives a diverging vertical response, apparently somewhat similar to Fig. 7(f). There are however more involved additional responses, as representatively shown in Fig. 7(b). Fig. 9 shows the impedance plane plots corresponding to the complex capacitance plots in Fig. 7, except for Fig. 7(h). Figure 7(h) shows the response at 1.8 V, while Fig. 9(h) shows the impedance response at 2.0 V. Fig. 9(h) indicates the low frequency feature described by a TL model, characterized by the slope-one, high frequency ‘Warburg’ impedance discussed below. The spectrum does not allow a deconvolution of the Schottky capacitance component. Two presentations in Fig. 7 and Fig. 9 illustrate that the overall impedance is successfully described by a Bisquert TL model (DX-22) in parallel to the HN capacitance function (DE-31), which is suggested as a physically plausible model for the Schottky contact of a semiconductor with possibly distributed trap levels.
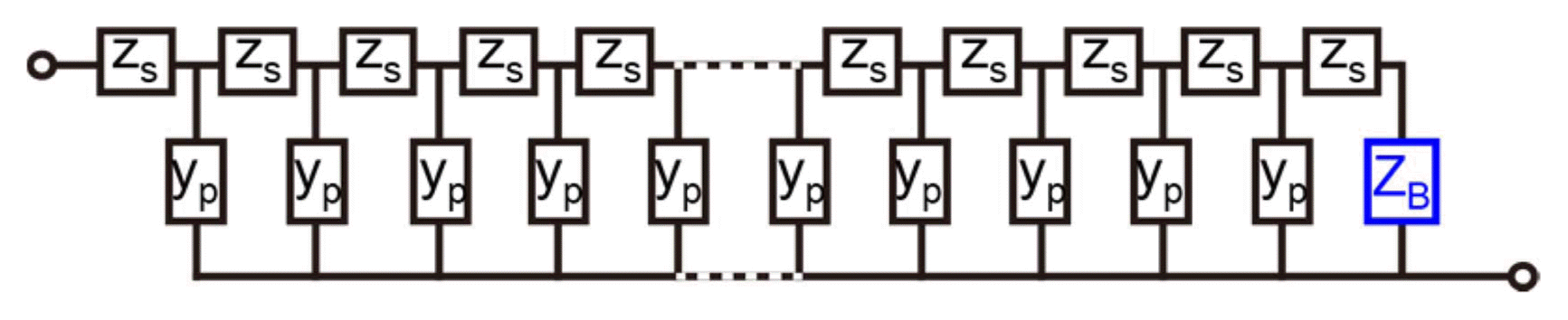
The Bisquert TL model employed in this work can be generally represented as is shown in Fig. 10:39) the longitudinal rail of impedance ZS = ∑ zs, admittance in transverse direction or shunt admittance YP = ∑yp, with the connected in series to ZS and in parallel to YP. The interfacial impedance ZB component has a special position in the TL model and cannot be located independently from it. A more generalized model may contain a finite impedance of the bottom rail, with an interfacial impedance ZA connected in series. When the bottom rail is of negligible resistance, ZA can be taken outside of the entire TL model. One type of the carriers is often indeed much more conductive than the other. The impedance of this general TL model is given by the following:
With ZB→∞, it becomes
For the electrochemical impedance of the porous electrodes, a simple theoretical model of three parameters RS, RP, and CP, as shown in Fig. 6, can be considered, i.e. ZS = RS = ∑rS,
when ZB(ω→0) → ∞. It applies to the Warburg impedance of infinite length as ZB in Fig. 6, as well as to the simple open-circuit. For the short-circuited, ZB(ω→0) → 0, the magnitude becomes less as
As discussed by Bisquert et al.,8,10) there is a degeneracy of TL models involving transport. As far as the small signal AC impedance is concerned, the model for porous electrodes in which the transport is by drift in the electrical field and the electrochemical reaction, e.g. following a Butler-Volmer relationship, occurs at the distributed interfaces, is equivalent to the diffusion-reaction(recombination) model. The actual physical mechanisms can be distinguished by examination of the behavior of the parameters in different conditions. The diffusion-recombination model has been successfully applied to DSSCs with low-doped nanostructured TiO2 electrodes, where no electrical potential gradient or electron drift is supposed to occur, as the electron charge in the nanostructured TiO2 is compensated by the positive ion charge of the surrounding electrolyte. Diffusion of the electrons and bulk recombination are concerned, as for the electron minority carriers in the p-region of the p-n junction. The same model has been applied to the porous gas electrodes of solid oxide fuel cells40) where the (surface) diffusion and adsorption reaction model by Mizusaki can be applied,41) rather than the charge transfer reaction model of traditional electrochemistry. It is also likely that additional TL model components are present such as the diffusion process within the liquid electrolytes in the classical electrochemical cells or DSSCs,4) or gas concentration phenomena in fuel cells.40) The identification of the respective TL components may not be trivial. Some indication of Warburg impedance in the electrolyte is given in Fig. 9(d) and (h), which is represented by a CPE in a dashed line in Fig. 6, with α = 1/2. The bent capacitor symbol or >>, originally suggested for the program LEVM by Macdonald,42) is employed in the ZView program.
In the porous electrodes electrical network model, CP represents the double layer capacitance proportional to the charge accumulation and the enlarged interface area of the porous structure. On the other hand, when the diffusion mechanism is involved, CP represents chemical capacitance, CCHEM
where n represents the carrier concentration per area or per volume, depending on the mechanism concerned. The geometry factor G becomes the surface area or the volume of the electrode material, respectively. The diffusion coefficient in Fick’s law (or the chemical diffusivity), reaction rate constant, and the effective reaction zone (or utilization length), can be directly derived by the three parameters of the TL model, RS, RP, and CP, as
(These derived parameters are presented in Fig. 12.) Effective reaction zone is represented by the ratio of RP to RS. With large RS, i.e. small DCHEM, the process is diffusion limited, and LEFF << 100%, that is, only a part of the electrode thickness is utilized. Large RP, that is, small kRXN, means small recombination in semiconductor solar cells. Consequent LEFF >> 100% or the entire electrode thickness being effective leads to the high performance for solar cells. On the other hand, both high transport and reaction rates are desirable for the electrochemical conversion. Around 50% utilization length has been found for SOFC electrodes.40)
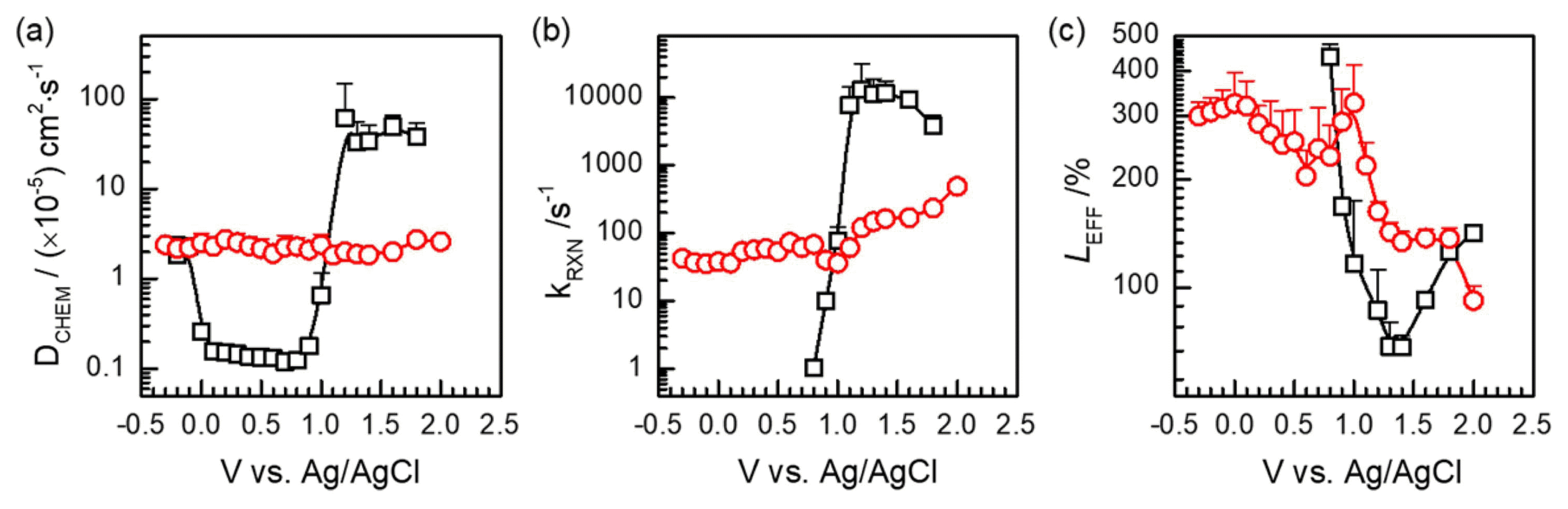
Chemical diffusivities (a), reaction rates (b), and effective thickness in percent (c), derived from the Bisquert parameters of RS, RP, and CP.
In the previous section, HN dielectric function was suggested for the dispersed Schottky capacitance behavior. Unlike the popular CPEs, the model allows the determination of well-defined capacitance parameters, which can be used for MS analysis. Bisquert’s group has played an essential and pioneering role in the rigorous derivation of the TL models and in the exhaustive and comprehensive associated physical interpretations. Much emphasis has been given on the capacitance parameters. Similarly, as for the Schottky capacitance, well-defined CP parameters are needed for the straightforward physical interpretations, such as double layer capacitance, or the chemical capacitance in Eq. (8). With CP together with RS and RP, the ideal, three-parameter Bisquert model is characteristic for the slope-one, high frequency behavior and semicircular, low frequency end with a vertical slope, as shown by the impedance spectrum in the blue line in Fig. 11(a), labeled as ‘wo QW’. In this case, the capacitance Bode plot should show a plateau as shown in Fig. 11(b). The plateau values approach CP when RP >> RS, or when the low frequency spectrum represents (RPCP) parallel circuit.

Simulation of the Bisquert element of Fig. 9(h) (EXP): RS = 3606 Ω, RP = 3054 Ω, CP = 0.6686 μF, QW = 8.3775 μF·s1/2. Simulations without QW element, with QP = 0.6686 μF·s0.2 and 6.686 μF·s0.2 (α = 0.8), and with HN capacitance of CHN = 0.6 μF, τ = 0.001 s, and γ = β = 1 as shunt capacitance, with and without QW, are compared in impedance plane (a) and capacitance Bode plot (b).
However, most of the real experimental data for the TL modeling cannot be described by the three parameters, RS, RP, and CP. The deviation is accommodated by the ‘useful’ and ‘indispensable’ CPEs,4)
which is probably more known and practiced in the impedance analysis45,46) than the original HN dielectric function. The model has been long since provided in the CNLS (now LEVM) program by Macdonald, and as the DE-6 model in ZView. Empirically, there has been little indication of closely correlated high frequency and low frequency dispersion behavior as required in Bisquert TL model with CPE.
As is in (RQ) modeling, the question arises how the capacitance magnitude, represented by Eq. (8), needed for the derivation of the kinetic parameters DCHEM and kRXN according to Eqs. (9) and (10), can be determined. As discussed above, the effective capacitance ‘C’ is defined by the peak frequency or time constant (RQ)1/α for the (RQ) parallel circuits as (R‘C’). Note that capacitance values are determined by the resistance parameters. Such correlation may not be rigorously justified. Moreover, for the TL model with two resistor components, RS and RP, it is not clear which resistor component should be used. The RSQP TL represents the diffusion mechanism, so the diffusivity for the anomalous transport or fractal diffusion is estimated from the relaxation time τd = (RPQP)1/α, while the recombination (reaction) rate is estimated from the time constant τrec = (RPQP)1/α. The feature of QP modeling is illustrated in Fig. 11. Two QP simulations are distinguished in the Bode plots (not in the impedance spectra). With the QP coefficient in
This issue was pointed out in the application of the Bisquert TL model for fuel cell electrodes40,47,48) and the Jamnik-Maier model for mixed conductors.49–51) With these issues taken into consideration, the electrode responses of full, high temperature fuel cells were described by four TL models in the ideal form with three parameters of RS, RP, and CP, which represented electrochemical polarization and gas concentration impedance for the anode and cathode, respectively.40) The apparent success in reasonably describing the spectra and systematically obtaining the parameters may be due to the strongly overlapped four TL responses. The strongly depressed semicircular responses for the symmetrical cells theoretically containing only two TL elements were difficult to describe with the Bisquert TL model with ideal capacitance parameter, CP.48) In order to compare two different current collectors the frequency exponent α of QP, was fixed to 0.5.48) The most obvious serious trouble with CPE modeling is that the other circuit parameters, as well as the coefficient Q in
This work suggests a more powerful and essential modification of the Bisquert TL model to be widely applicable to experimental data, and also providing clear physical interpretations. As indicated in the spectrum of Fig. 9(h), slope-one behavior is often clearly indicated in the high frequency region, which is not consistent with the depressed arc behavior of the low frequency region according to Bisquert TL model with QP. Slope-one behavior is a clear indication of the ideal form of shunt capacitance CP, which is also desirable for the unambiguous physical interpretation of DCHEM and kRXN. It turned out that such inconsistency in high and low frequency behavior could be successfully described by the presence of infinite length RC TL or Warburg impedance as the interfacial impedance ZB in Fig. 10, as shown in the equivalent circuit of Fig. 6. The modeling was motivated by the indication of the universal presence of the ideal Warburg electrode response in the impedance of polycrystalline solid electrolytes.25,27,28) Note that the infinite length RC TL for ZB requires only one parameter, since the impedance of infinite TL is
The impedance spectrum of Fig. 9(h) represents the TL model response directly, as the HN capacitance component cannot be reliably separated, i.e., the spectrum does not need that component for the description. That TL response of the 4 fit parameters RS, RP, CP, and QW is shown in Fig. 11, labeled as EXP. All the spectra in Fig. 11 use the same RS and RP. In Bode plots of Fig. 11(b), the effect of the QW element is clearly shown. While the response without QW, the blue line labeled “wo QW”, indicates a well-defined capacitance plateau at low frequencies, QW adds the sloped behavior close to −1/2. The capacitance effects are additive, as can also be seen in the equivalent circuit of Fig. 6. The high frequency response is shown to be essentially described by RS, RP and CP, regardless of ZB. Note that for any QP with α < 1 as ZB, or as long as no shunt conductance or interface ‘leakage’ exists, i.e. ZB(ω → 0) → ∞, the magnitude of TL is determined by RS and RP as
Similarly as discussed above for the Schottky capacitance, the HN capacitance function with well-defined, low-frequency limiting magnitude can be a generalized CP. With γ = β = 1, the model represents a trapping process described by RC series circuit. Without RP (or Rp → ∞) this corresponds to the diffusion-trapping process, one of the diffusion-related processes considered by Bisquert.6) Generally, the model contains parameters for drift, diffusion, (generation) recombination, and trapping processes much discussed in semiconductor device physics.14,15) Note that with the same RS and RP, the capacitance distribution, for example due to trapping, leads to well-distinguished two arcs, as shown in Fig. 11, for τ = 0.001 s and CP divided into an HN contribution of 0.6 μF. Modified Bisquert models with an HN function as a general shunt capacitance, are newly available as DX-25, 26, and 27, in ZView software program (version 3.5e). The additional effect of QW depressing the semicircular responses is also presented. Note that such spectral features are generally described by (R1Q1)(R2Q2), and it is attempted to separate two resistance components R1 and R2 constituting the total resistance as R1 + R2. In contrast, the overall resistance of TL containing two resistance components, RS and RP, is represented by Eq. (6). It may be noted that the distributed CP and the interfacial capacitance are all additive. This is also in line with the recent suggestion of the superiority of additive capacitance effects in parallel network in describing polycrystalline solid electrolytes to the conventional additive resistance effects in series network, well known as brick-layer model.25–28)
3.5. TL Mechanisms
When the polarization resistance RBQ is small at high reverse bias close to 2 V, as shown in Figs. 9(d) and (h), the presence of additional low frequency Warburg impedance is indicated. In Fig. 6, the component is shown by the dotted CPE Q element, with α = 1/2 in series to the parallel connection of DE-31 and DX-22. The component represents RC TL. (It should be distinguished from ZB within Bisquert TL (DX-22).) The response is attributed to the mass concentration impedance in the electrolyte solution, present in all electrochemical cells that have liquid electrolytes. The component is not affected by the potentials or illumination, but can be observed when the electrode polarization resistance becomes small enough.
As discussed previously, the origin of Bisquert TL (DX-22) in parallel to Schottky capacitance, represented by HN dielectric function (DE-31), should be considered two-fold: drift or diffusion; charge transport in the electrochemical network of porous electrodes, or by the diffusion-recombination mechanism of electrons in TiO2, represented by Eqs. (8)–(10), following the mechanism in DSSCs. In the latter, no electrostatic potential gradient within the low-doped nanostructured TiO2 electrode layer is assumed. The mechanism also requires a particle size of a few tens of nanometers, so that the charges are compensated by ionic charge at the TiO2/electrolyte interface. The condition seems not to be met in the case for TiO2 nanorods of the microstructure schematically shown in Fig. 4 and also due to the presence of Mott-Schottky behavior shown in Fig. 8.
According to the diffusion-recombination model applied to nanostructured TiO2 electrodes in DSSCs, donor concentration n of the low doped TiO2 depends exponentially on the applied (reverse) voltage as exp(−qV/kT), since the applied voltage can homogeneously change the Fermi level of the nanostructured TiO2, while the charge neutrality is maintained by the positive ion charge at the semiconductor/electrolyte interface.10) According to Eq. (8)CP, being proportional to n, should have the same dependence. In the simple approximation, the transport resistance, RS, inversely proportional to the conductivity, and the recombination resistance, RP, inversely proportional to the electron concentration, they are all proportional to exp(+qV/kT). It corresponds to the very large negative or positive slope of 17 in the logarithmic values of the parameters vs. V at room temperature. In Fig. 6, the correct sign but much weaker dependence (< 1) is indicated in the parameters RS, RP, and CP, at the potential less than 0.7 V vs. Ag/AgCl. The observation is quantitatively comparable to the behaviors of the aged DSSCs, or DSSCs with highly doped TiO2.9) Fresh DSSCs exhibited stronger dependence, but still less than the theoretical value. The aged behavior was attributed to the doping during the operation. It is notable that the opposite variations in RS, RP, and CP, occur above 0.7 ~ 1.0 V vs. Ag/AgCl, where the leakage or breakdown becomes predominant upon reverse bias. The dependence is shown to be more or less symmetrical under the illumination condition (red circles), while abrupt change occurs in the dark condition (black squares).
Figure 12 shows that the diffusivity DCHEM in the dark condition becomes almost constant and small between −0.1 V to 0.9 V in the reverse bias region, and a stepwise increase by 500 times above 1.2 V. The dependence originates from RS and CP, which are high in the region of forward bias direction and low in the high reverse bias. Reaction rate constant kRXN behaves similarly. In the forward bias region, kRXN is not obtained since RP is too large to be determined. On the other hand, DCHEM becomes independent of the potential under illumination. DCHEM is also constant in the respective potential ranges under the dark condition, i.e. V < 0.9 V and V > 1.2 V. That means the characteristic variations of RS and CP with potential are exactly opposite in logarithmic scale. This is because both
The characteristic DCHEM behavior under illumination suggests an almost symmetric n-p transition. The electron and hole concentration follow exponential dependence of potential, which is related to the Fermi potential of electrons and holes, EFn, EFp, respectively. Importantly, the variation of the carrier concentrations under illumination is supposed to concern the TiO2 volume responsible for the observed resistance and capacitance values. On the other hand, the absolute values of RS, RP, and CP, in the dark condition above 1 V are considered to be affected by the inhomogeneous conduction pathways of breakdown spots, as also indicated by currents not scaled with the area as discussed earlier for Fig. 2. The leakage or breakdown behavior under high reverse bias are strongly affected by the film quality and the state of thesubstrate/TiO2 interface.
In conclusion, the Bisquert TL parameters qualitatively indicate the diffusion-recombination mechanisms of electronic charge carriers in TiO2. Combination of Schottky capacitance and diffusion-recombination response may not necessarily be contradictory or incompatible. Note that these mechanisms work together in semiconducting structures with depletion of majority carriers at the junction and with the transport of the minority carriers in the bulk.14,15,16) Nanostructured TiO2 and ZnO electrodes show diffusion-recombination processes in the forward bias region in the aqueous solution used for photoanodes of PEC cells, as well as in the organic electrolyte for the DSSC application.13,53,54) On the other hand, MS analysis is routinely performed in the reverse bias region for identical or similar nanostructured electrodes. There is no abrupt boundary between high and low doping cases, or between meso- or macroscale and nanoscale. Spatial inhomogeneity in the electrode responses may also exist, e.g. at top vs. lateral surface vs. inner volume of the TiO2 nanorods, due to the crystal anisotropy, surface chemistry and structure and/or inhomogeneous doping concentration. Therefore, it may be concluded that, due to the inhomogeneity in the material, or in the potential distribution, and/or in the case of moderate doping level, the two mechanisms are generally coexistent, as represented by the master equivalent circuit in Fig. 6 for semiconducting photoanodes of PEC cells.
The presence of interfacial Warburg impedance as ZB is the important modification of Bisquert TL model for a wide applicability. The behavior of QW parameter in Fig. 6 suggests a very close relationship to the bulk diffusion mechanism, as the estimation of
Although the ideal CP parameter is used in the description of all spectra, the characteristic slope-one behavior can be directly found in only a few spectra at high reverse bias, e.g. Figs. 9(d) and (h). There are three factors to be considered for such a feature. First, when RS is much larger than RP, or DCHEM is much smaller than kRXN, the slope-one behavior becomes dominant in the TL model response. This diffusion-limited response corresponds to the effective reaction zone or to the utilization length of substantially less than 100%. Secondly, slope-one behavior can be identified in the small portion at the high frequency range, which is likely to be overlapped with other high frequency components such as ROHM and L and other stray impedance. Thirdly, often the high frequency slopes greater than one results from the overlapping capacitance effects. In the present work the deviation is explained by the Schottky capacitance connected in parallel. Similarly, it has been pointed out that the high-frequency feature of the Warburg impedance of the Hebb-Wagner polarization cells is affected by the double layer capacitance due to the blocked species which is positioned similarly as QW.49,50) The manifestation of diffusion components in the spectra in Figs. 9(d) and (h) can be ascribed to the negligible contribution of Schottky capacitance at high reverse bias, according to MS behavior. It should be noted that the two capacitance parameters representing each mechanism, CSB and CP, are comparable in magnitude, but the respective characteristic potential dependences are well presented. The results can be considered to indicate the successful separation of the two impedance mechanisms.
4. Conclusions
Full parametric impedance analysis of the AC response of a TiO2 photoanode in a PEC cell, as a function of the potential and with varied illumination condition, has been performed. Essentially, two capacitance components are connected in parallel: depletion capacitance at the semiconductor-electrolyte junction following an MS relationship, and chemical capacitance in the TL model for the electron diffusion-recombination kinetics in the bulk TiO2. Well-defined capacitance parameters can be found by employing an HN capacitance function, which represents the distributed trap levels of a finite concentration. The Bisquert diffusion-recombination TL model can be applied with chemical capacitance in ideal form, not as CPE, allowing a straightforward interpretation of the diffusivity and recombination rate constant. Interfacial Warburg impedance, closely related to the bulk diffusion mechanism, successfully explains the depressed semicircular responses of the experimental data. The 4-parameter Bisquert TL model is suggested as being generic and widely applicable.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2017R1D1A1B03033918) and by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science, ICT & Future Planning (NRF-2014R1A2A2A04004950).
Notes
The authors certify that there is no authorship dispute between them.
DX-22 (Bisquert #3-2) recently added, modified from DX-12 (Bisquert #3), has essential parameters in smaller number. The allows the multiparameter, full cell model as shown in Fig. 6 to be run within the 30 parameter limit in the equivalent circuits of the ZView program.