1. Introduction
Perovskite oxides have attracted much interest due to their possible uses in proton conducting fuel cells.1-26) The traditional mechanism for proton incorporation in perovskites is directly tied to the dopant concentration.15,27) When an ABO3 perovskite is doped at the tetravalent B sites with trivalent ions, an oxygen vacancy results for every two doped sites. This vacancy dissolves water from the atmosphere into a hydroxyl, which fills the vacancy and a proton which quickly binds to an oxygen in the perovskite lattice. Both protons freely conduct through the oxygen ion network of the perovskite. Since the mechanism suggests a 1 : 1 ratio of protons to trivalent dopant ions, previous proton conduction simulations in perovskites have considered only one proton and one dopant simulations.4-13,15-26) However, one study28) on a different perovskite system finds low energy minima in a perovskite with protons only 2.3 Å apart due to lattice relaxation as well as pathways for moving the two protons together. The same study uses a simplified model to show that the two proton motion may in fact be the dominant diffusing defect.
This paper uses KMC to explore if a system with multiple protons initially placed far from each other can result in protons in close proximity. Additionally, the paper discusses the effect of a second proton on the probable paths of the first using graph theory and DFT on a small system. One might expect that an excess proton could change conduction by occupying the lowest energy binding sites, causing lattice distortions, and/or providing alternative conduction mechanisms through correlated proton motions. These could potentially decrease or increase conduction. To assess the impact of an excess proton on the conduction of a probe proton, this paper calculates the binding and transition state sites of a probe proton using the same electronic structure methods as used in an earlier paper for a single proton.25)
In principle, both the excess proton and the probe proton move through the lattice. Since a proton can bind to an oxygen in a perovskite with four possible hydroxyl orientations, 23-26) after one proton is added to the system, there are only N-4 possible sites for the second proton where N is the total number of binding sites. As a result, there are N (N-4) / 2 combinations of two protonated sites when two protons are in the system. Since the total number of sites in our earlier single proton studies25) is 96, there are 4,416 possible combinations of two protons in this system. Finding the minimum energy for all those combinations and the transitions between them is not practical. As an approximation of the effect of an excess proton on a probe proton’s motion, we will simply fix the position of our excess proton at the best binding site for a single proton and consider the pathways of the probe proton based on energetics alone.
Conduction pathways for the probe proton are then found using graph theory. Each binding site is a vertex in a graph. Vertices are connected by edges when a single transition state exists between them. Probabilities for the pathways are assigned using a Boltzmann probability for the initial binding site and conditional probabilities based on approximate rate constants for moving through the remaining vertices in the path. Dynamic programming is used to search for all pathways through the vertices as in our earlier work.25,26)
Section II A describes the KMC29,30) approach used while section III A describes the resulting trajectories in systems with multiple protons with an equal number of dopant ions. Sections II B and III B describe how the binding sites, transition states, and rate constants are calculated and how they change with the presence of an excess proton, respectively. Sections II C and III C describe how long range proton pathways are calculated through graph theory and how the excess proton affects the long range conduction paths of the probe proton, respectively. These results suggest that proton motion is correlated and the first proton may prepare the way for the next.
2. Computational Procedure
2.1. Kinetic Monte Carlo including field generated by charged defects
The 12.5% Y doped BaZrO3 proton binding and transition state structures and energies found in our earlier study25) were used in a KMC study using the approach of Pornprasertsuk et al.30) In this approach, the effective barrier between binding sites is shifted by half the electric potential difference between the binding sites. The total electric potential at each site includes a contribution due to the fields created by charged defects as well as the applied field. Both of these contributions are calculated for planes perpendicular to the applied field. The new effective barrier is used to find the rate constants used in traditional KMC.29)
A 2 × 2 × 2 unit cell unit was replicated along the z-axis to form longer systems. Systems of one, two, four, and eight units were considered. This creates KMC simulation cells of length of 8.52, 17.04, 34.08, and 68.16 Å. The width and depth of the cells is 8.52 Å. Each original replicated unit contained one yttrium dopant ion. At the start a proton was placed in the lowest energy binding site in each replicated segment so that there are an equal number of protons and dopant ions.
The Vienna ab initio simulation package (VASP)31,32) was used in our earlier study25) to find the energies and normal mode frequencies at all the original unit binding and transition states. Specifically, the DFT method with the Perdew-Burke-Ernzerhof (PBE) functional was used to perform conjugate gradient optimization to find binding site energies and the Nudged Elastic Band (NEB)33) method was used to find minimum energy pathways between binding sites. The climbing NEB method33) was used to find the transition state. Finally, the dynamical matrix method34) was used to find normal mode frequencies at the binding and transition states. Details on these calculations are given in our earlier study.25) In this paper, we use the energies, barriers, and frequencies found for the original 2 × 2 × 2 unit cell system25) within the replicated longer systems.
The defect interactions between the z-replicated original system units are included in the electric potential contributions of the charged defects as described in the Pornprasertsuk KMC approach.30) The charged defect (proton and yttrium dopant) contribution includes the relative permittivity for barium zirconate which varies from 15 to 120 depending on experimental and calculation conditions.35-40) References38,40) find the relative permittivity under conditions closest the system in this study (bulk and in Glazer (-,-,-) configuration) to be about 50, the value used in this simulation. The charge defect interactions damped by the relative permittivity along with the earlier DFT data were used to find the rate constants for proton motion between all binding sites. These rate constants were used in the KMC approach.
2.2. Binding and transition state calculations
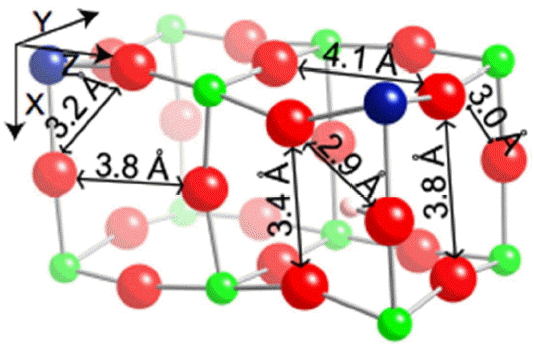
As seen in our earlier study25) of 12.5% Y doped BaZrO3, the presence of a proton affects the structure of the lattice. Locally, oxygens get closer to the hydroxyl site making the interoctahedral distance closest to that site 3.4 Å rather than the more standard 3.8 Å in doped faces. This creates hydrogen bonds of about 2 Å. There are also some contractions of intraoctahedral OO distances near the excess proton. Further, as seen in the Fig. 1, interoctahedral transfer distances increase to 4.1 Å in the YZ plane making this plane’s distortions very similar to those in undoped planes. Earlier studies25) showed that proton conduction pathways without an excess proton have a significantly higher probability of occurring in the distorted doped planes. The increased interoctahedral distance in the YZ doped plane which effectively decreases the YZ plane’s distortions indicates that the presence of a proton could significantly impact the trajectory of another.
To find the effect of an excess proton at the lowest energy binding site on the energies of other binding sites, a probe proton was placed at each of the other possible binding sites and the energy was minimized. The same electronic structure methods as in our prior work25) which were briefly described in the previous section were used. However, with two protons and only one doped ion, a homogenous background charge of −1 is used to preserve charge neutrality. The NEB method33) was used to find transition states between neighboring binding sites using 2-6 intermediate images.
Using the binding and transition states found, rate constants are calculated using the standard harmonic transition state theory formula of
k i → j ( T ) = A i → j exp ( - E i j - E j k B T )
Ai→j is the prefactor or the frequency of i → j attempts. Eij is the energy of the transition state between binding sites i and j. Ei is the energy of binding site i. As seen in our earlier studies,25) fixing the transition state energy pre-factor for all transitions at a constant value does not significantly affect the most probable pathways found and their average properties. For simplicity, we will fix the prefactor at 1 ps−1 for all transitions and effectively only consider the energetics of the pathways. The probability of moving from site i to site j given that the probe proton starts at site i (pi→j (T)) is the rate constant normalized by all the possible escape routes or
k i → j ( T ) ∑ j = 1 M k i → j ( T )
2.3. Finding long range proton pathways in the presence of an excess proton
Proton conduction pathways are found using a dynamic programming recursion on path weight to search the binding and transition state graph as in our earlier work.25,26) The binding sites are the vertices of the graph. These are connected by an edge only if there is a single transition state between them. In this and earlier papers,25,26) long range conduction pathways are defined as those that start at a binding site or vertex and end at a periodic image of that binding site traversing the entire simulation box. These pathways can be periodically replicated to achieve long range conduction. If the periodic pathway contains n steps, it is said to be n-step periodic. In another study, we find that this definition captures the essential features of long range conduction pathways.41) The overall probability of such an n-step periodic path (i1, i2, …in, i1) is ρi1 (T)pi1→i2(T)…pin→in(T)pin→i1 (T) where ρi1(T) is the probability of being at site i1 at temperature T or the Boltzmann distribution at that site. The weight of the path, a more convenient quantity in the dynamic programming recursion, is minus the natural log of the probability of that path. The individual edge weights between sites i and j are wi → j (T) = − ln pi → j (T).
The n-step periodic path (i1, i2, …in, i1) has n − 1 vertices between the starting and ending points and n distinct vertices. Dynamic programing is used to go through all subsets (S) of n distinct vertices and find the minimum weight of a path that starts at i1, visits the vertices in the subset once and ends at a vertex connected to the original vertex. Since all subsets are considered, all subsets with non-zero probability or non-infinite weights are kept and subsequently sorted.
To consider all subsets, we start paths at i1, define an array R with all vertices except for the first one, loop through all vertices j in R keeping only those that connect to the previous vertex. If vertices i and j are connected, pi → j (T ) is non-zero and wi→j is finite. All possible one step paths (i1, i2) are stored along with the current weight for that path. After only one step, the path weight would be ωi1→i2(T). The next iteration considers all the connections to the second vertex in the currently stored paths. An array (R) with all vertices except for those already visited is defined. All possible next vertices from that array are considered and only those with edges connecting to the previous step are kept. Paths are duplicated when multiple next steps are found and terminated when there is no next step found. The latter is equivalent to finding only infinite weight edges. The path list is updated with all the new vertices and the path weights are increased by the new edge weight. The process continues until the paths have n vertices. In the final step, only the paths whose in vertex connects to the original vertex and that span the simulation box are kept. The path weights are augmented by − ln(ρi1 (T)) + wi1 →i (T)). The vertices removed from the array R for each path comprise the subset S for that path. All the paths found are sorted by probability or weight.
This algorithm is effectively what Scott et al.42) describes as dynamic programming using the overall path weight recurrence Wi1(S,T) = mini∈S−{i1} Wi(S−{i1}, T) + wi1→i(T). The recurrence has been written in the notation of this paper. A final weight of −ln (ρi1 (T))+ win→i1(T) is added to get the overall path probability in this physical setting. The final weight considers the probability of the initial vertex and the probability of the final connection from in back to the initial vertex. All possible initial vertices are considered. While the recurrence finds the minimum weight path, all possible n step paths are stored and sorted in order of increasing weight or decreasing probability. The stored paths are the ensemble of possible n-step periodic paths at temperature T. The ensemble contains the same paths in the forward and backward direction with equal probability.25)
Separate searches are done for each length path. To estimate the preferred periodic length, average estimated times for each length path can be found when rate constant prefactors are available.25,26) For this rough estimate of the effect of an excess proton on the conduction of a probe proton, estimated times are not calculated and a purely energetic assessment is made.
3. Results and Discussion
3.1. KMC trajectories show protons in very close proximity altering pathways
Kinetic Monte Carlo million picosecond trajectories at 1000 K were obtained for the original system replicated one, two, four and eight times in the absence of an external field. Initially, protons are placed in binding sites 8.52 Å apart along the longest side of the simulation box. The simulation box is periodic along the shorter two lengths. When a proton exits the replicated simulation box through the z-direction, a proton is added to the first layer on the z-axis based on the Boltzmann probability of having sites on that layer occupied. The process is repeated until the simulation time exceeds a million picoseconds. Limiting barriers were found by keeping a log of the barriers for protons traveling from entry to exit. The highest barrier seen in each proton trajectory was the limiting barrier for that proton trajectory. Over the million picoseconds of the simulation, many individual proton trajectories were found. To get the limiting conduction barrier, the individual limiting barriers were averaged weighted by the fraction of the time spent in their trajectory. The average limiting conduction barriers found at 1000 K for one, two, four, and eight proton systems were 0.39, 0.43, 0.44, and 0.45 eV, respectively. Intraoctahedral transfer limiting barriers represented 86%, 96%, 95% and 93% of the limiting barriers, for 1, 2, 4 and 8 proton systems, while rotational limiting barriers represent 12%, 2%, 0%, and 0% of limiting barriers, respectively. Finally, interoctahedral transfer limiting barriers represent 2%, 2%, 4%, and 7% of limiting barriers, respectively. This changing percentages of limiting barrier types for long range paths suggest that the presence of multiple protons alters chosen pathways.
When a field of 0.12 V/Å is added, the average limiting barriers change to 0.32, 0.35, 0.38, and 0.41 eV for 1, 2, 4, and 8 proton systems, respectively. This is a decrease relative to the zero field case as expected. More interestingly, the percent of each type of limiting barrier also changes. With the field, intraoctahedral transfer limiting barriers represent 56%, 69%, 81% and 89% of the limiting barriers, for 1, 2, 4 and 8 proton systems, while rotational limiting barriers represent 43%, 29%, 17%, and 9% of limiting barriers, respectively. Finally, interoctahedral transfer limiting barriers represent 1%, 1%, 2%, and 2% of limiting barriers, respectively. Overall, the field leads to more rotational limiting barriers and fewer intraoctahedral transfer limiting barriers. However, as protons are added, their motion along with the fixed lower valency dopant defects can create fields opposing the applied field. The competing effect of having more protons once again leads the intraoctahedral limiting barriers to become dominant. Once again, we see that protons affect the trajectories of other protons.
Let us consider the effect of the applied field in more detail. As in our earlier single proton work,45) the dopant defect acts as a trap for the proton. Occasionally, the trap is escaped through a long range limiting barrier which is most often an intraoctahedral transfer and less often a rotation. In the absence of field, the deepest potential energy wells are near the dopant though the trend is not monotonic. The field applied along the z-axis decreases the energy barrier to forward moves, increases the energy barrier to backward moves and leaves barriers to moves on planes perpendicular to the z-axis or field constant. The net effect is a tilting of the potential energy map lowering the region near the negatively charged electrode. This changes individual barriers differently. Using a flow of charge analogy and keeping in mind that the system has connections both in the field direction and in the planes perpendicular to it, the choke points in the charge transport can change as a result of the potential energy tilting. In fact, the proton residence time in some planes perpendicular to the field decreases while it increases in others due to multiple minima with different barriers and connections. The different planes have different connections to other planes leading to alternative routes and hence changes to the fraction of rotation and transfer limiting barriers. The 0.12 V/Å field tends to shift the residence time distribution and its choke points in the direction of the field moving the largest choke points from dopant planes to planes just after the dopant.
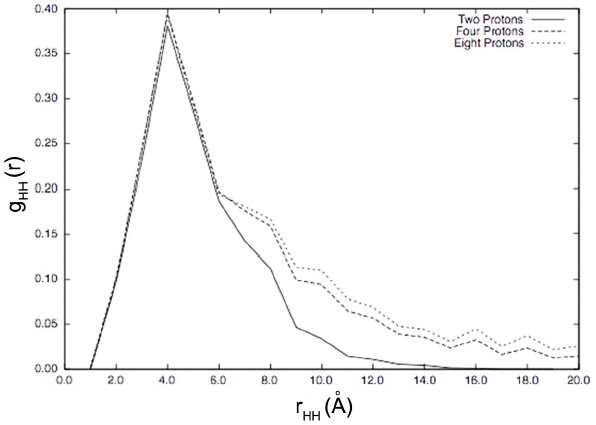
For all multiple numbers of protons, the proton-proton radial distribution shows a significant broad peak at about 4 Å as shown in Fig. 2. This broad peak shows that protons can get as close as 2 Å from each other. Since the energies used in this KMC simulation came from single proton DFT calculations with only the addition of proton/proton interactions through electric potential contributions of defects summed through planes of the simulation box, we next consider including the effects of additional lattice distortions by doing additional DFT calculations on the original small 2 × 2 × 2 unit cell system with the addition of a second proton.
3.2. Protons affect the binding sites, transition states, and rate constants of nearby protons
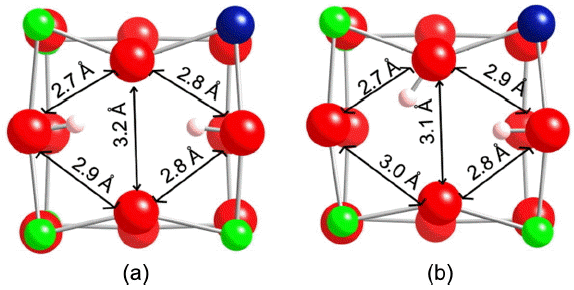
The binding sites found look very similar to that of the original system. Only binding sites on oxygens without the excess proton are considered. Not surprisingly, binding sites on the same oxygen as the excess proton led to movement of one of the protons to a nearby oxygen. Protons on sites near the excess proton form hydroxyls which are tilted away from the excess proton. The probe proton distorts the lattice in a similar way to the excess proton but also is affected by the initial distortions made by the excess proton. For example, the lowest energy binding sites are on the same face as the excess proton as shown in Fig. 3. Comparison with Fig. 1 shows that the probe proton allows for continued contraction of OO distances. The optimized two proton positions allow for significant hydrogen bonding for the probe proton and the excess proton. The proton/proton distances in the lowest and second lowest binding sites for the probe proton shown in Fig. 3 are 2.68 Å and 2.16 Å, respectively.
Interoctahedral transitions through OO distances larger than 4.0 Å often proceeded through two intraoctahedral transfers rather than one interoctahedral transfer even with the smallest number of images. As a result, only interoctahedral transitions between oxygens closer than 4.0 Å were considered when finding paths. This resulted in considering only interoctahedral transfers in planes containing the oxygen binding the excess proton, namely the XZ and XY planes in Fig. 1.
In our earlier work,25) without an excess proton, transitions to doped octahedra were preferred over transitions away from doped octahedra. While the proton is still repelled less by the Y3+ dopant ion than by the Zr4+ ion, there are now additional factors to consider. The probe proton is also repelled by the positive charge of the excess proton. At the same time, the lattice distortions made by the excess proton stabilize some sites near the excess proton by allowing increased hydrogen bonding. Most forward and backward barriers follow the same patterns seen before the addition of the excess proton. However, some are changed by the additional competing factors of repulsion by the excess proton and stabilization of some sites near the excess proton. This results in some barriers for moving away from the dopant being lower in energy than the reverse barriers.
3.3. The excess proton affects the proton conduction paths of the probe proton
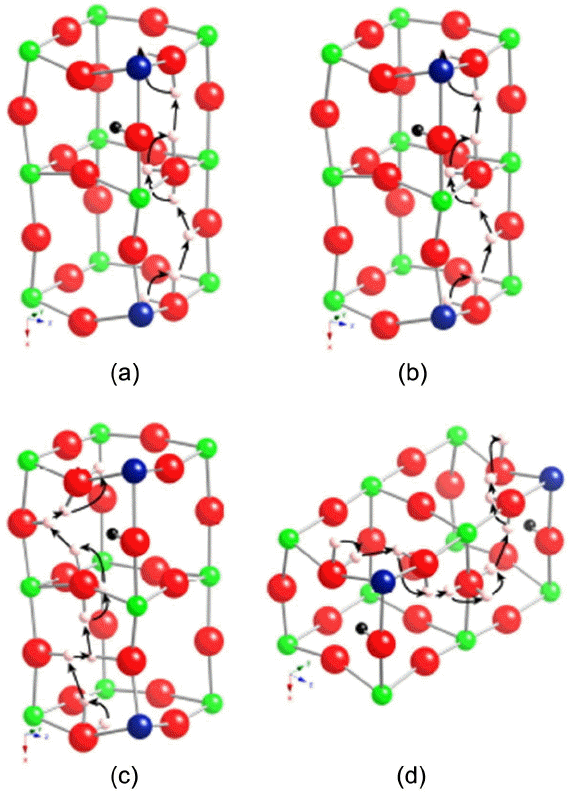
Figure 4 shows several probable probe proton conduction pathways at 1100 K given that the excess proton is fixed at the lowest energy single proton binding site. These are a small sampling of the many probable pathways. For periodic paths with 7-10 steps, the average limiting barrier through the paths is in the range of 0.31 to 0.41 eV. For comparison, the range for these same path lengths when a single proton is considered is 0.31 to 0.33 eV. A simple average between all path lengths considered suggests activation barriers of 0.32 eV and 0.37 eV in the absence and the presence of an excess proton, respectively. Like the KMC trajectories, dynamic path searches for a probe proton in the presence of an excess proton show an increase in average limiting barrier to conduction. The distribution of limiting step types, however, is less clear for this method as it varies widely by length of periodic path. The artificial selection of path length to odd numbers forces more interoctahedral limiting barriers as seen in our earlier studies.25,26) The odd numbered step periodic pathways often take a single interoctahedral transfer step (I) in preference to two intraoctahedral transfer steps (TT) and as a result have a sizable fraction of interoctahedral transfer path rate limiting steps. This shortcut leads to higher limiting barriers for odd numbered paths than even numbered pathways. In contrast, even numbered step periodic pathways have a very small fraction of interoctahedral rate limiting steps with and without the excess proton. Paths are limited by both rotations and intraoctahedral transfers. The excess proton increases the fraction of intraoctahedral transfer limiting paths for the 8-step periodic pathways while decreasing it for the 10-step periodic pathways. The fraction of rotation limited pathways is shifted in the opposite direction. Even numbered step paths in all directions are seen in the presence and absence of an excess proton. The excess proton slightly biases 8-step periodic paths in favor of the x-direction and 10-step periodic paths in favor of the z-direction. Overall, the excess proton impacts the probable probe proton pathways. Future investigations are underway considering different excess proton locations and concerted motions.
4. Conclusions
KMC simulations show an increased limiting barrier to proton conduction with increasing number of protons at 1000 K. The barrier starts at 0.39 eV with a single proton and reaches 0.45 eV with eight protons. The number of protons also affects the distribution of limiting barriers among the three possible step types: rotations, interoctahedral transfer, intraoctahedral transfer showing that protons affect the trajectories of other protons. Further, the proton-proton radial distribution function found for these trajectories shows a broad nearest neighbor peak at 4 Å with some proton-proton distances as small as 2 Å despite initial proton distances of 8.52 Å. The presence of multiple protons also increases barriers in the presence of an external field though the overall barriers are smaller than without the external field. Further, the field does not impact the radial distribution function significantly.
Since the KMC simulation treats proton-proton interactions approximately and does not consider additional lattice distortions added by additional protons, binding sites, transition states, and conduction pathways for a probe proton in the presence of an excess proton have been found using DFT with the PBE functional. The lower energy binding sites for the probe proton are near the excess proton. This allows the probe proton to make effective use of the already slightly distorted lattice and suggests that proton motion is correlated when there are multiple protons present. The probable conduction pathways reveal that the first proton raises the average periodic path-limiting barrier. The rise is not as great as with the KMC calculation because this path calculation only looks at paths of a probe proton around a single excess proton with fixed location and hence does not sample all the possible pathways. A simple average between all path lengths considered at 1100 K suggests activation barriers of 0.32 eV and 0.37 eV in the absence and the presence of an excess proton, respectively.
The experimental activation barrier in the 900 - 1300 K temperature range is 0.44 eV17,43) which is in excellent agreement with our 1000 K KMC average limiting barrier range for 2-8 proton systems of 0.43 to 0.45 eV and higher than the single proton KMC limiting barrier of 0.39 eV. Prior calculations with a single proton have found overall conduction barriers of about 0.3 eV.5,25) and some individual interoctahedral barriers of about 0.4 eV.6,25) The graph pathway search yields lower limiting barriers the KMC though still increasing in the presence of an excess proton. Graph pathway searches for periodic pathways lead to more direct pathways than KMC trajectories and often have lower limiting barriers.44,45) The advantage of having done DFT calculations in the presence of two protons was the revelation that the probe proton benefits from the lattice distortion that the excess proton introduced.